Bạn Cúc muốn pha 2 loại nước cam - Bí quyết pha chế chuẩn vị

Bài toán về việc pha chế hai loại nước cam của bạn Cúc là một bài toán phổ biến trong các đề thi hoặc bài tập liên quan đến bất phương trình và toán học ứng dụng. Bài toán thường đưa ra các điều kiện về số lượng bột cam cần thiết để pha chế hai loại nước cam khác nhau và yêu cầu người giải thiết lập bất phương trình để tìm ra số lượng nước cam có thể pha chế được.

Các điều kiện ban đầu

• Để pha một lít nước cam loại I, cần \(30 \, \text{g}\) bột cam.
• Để pha một lít nước cam loại II, cần \(20 \, \text{g}\) bột cam.
• Số lượng bột cam mà bạn Cúc có không được vượt quá \(100 \, \text{g}\).

Thiết lập bất phương trình

Gọi \(x\) là số lít nước cam loại I và \(y\) là số lít nước cam loại II mà bạn Cúc có thể pha chế. Chúng ta có các bất phương trình sau:

• \(30x + 20y \leq 100\)

Đơn giản hóa bất phương trình thứ ba, ta được:

Biểu diễn miền nghiệm

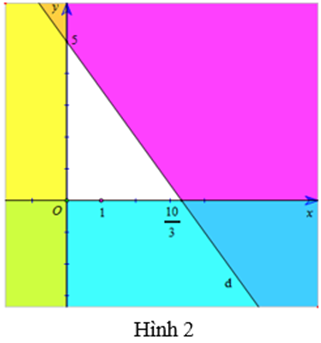
Miền nghiệm của hệ bất phương trình này được biểu diễn trên hệ trục tọa độ \(Oxy\) như sau:

• Miền nghiệm của \(x \geq 0\) là nửa mặt phẳng bên phải trục \(Ox\).
• Miền nghiệm của \(y \geq 0\) là nửa mặt phẳng phía trên trục \(Oy\).
• Miền nghiệm của \(3x + 2y \leq 10\) là nửa mặt phẳng dưới đường thẳng \(3x + 2y = 10\), bao gồm cả bờ.

Ứng dụng thực tế

Bài toán này giúp học sinh rèn luyện khả năng lập bất phương trình và biểu diễn miền nghiệm trên hệ trục tọa độ. Các bài toán kiểu này thường có tính thực tế cao, giúp người học hiểu sâu hơn về cách sử dụng toán học để giải quyết các vấn đề thực tiễn.

Bạn Cúc muốn pha hai loại nước cam với tỉ lệ hoàn hảo, để có một thức uống thơm ngon và bổ dưỡng. Việc pha chế này đòi hỏi sự kết hợp khéo léo giữa lượng bột cam và nước, nhằm tối ưu hương vị và chất dinh dưỡng. Trong quá trình này, mỗi loại nước cam có thành phần và tỉ lệ khác nhau, giúp mang lại sự phong phú về vị giác và cảm giác sảng khoái.

Loại nước cam thứ nhất cần 30g bột cam cho 1 lít nước, trong khi loại thứ hai chỉ cần 20g bột cam cho cùng lượng nước. Để có được hỗn hợp vừa ý, cần xác định lượng bột và nước sao cho cân đối và đảm bảo hương vị đồng nhất.

Để pha chế hai loại nước cam với các yêu cầu nhất định về lượng bột cam, ta cần có công thức cụ thể cho từng loại. Dưới đây là chi tiết cách pha hai loại nước cam.

Công thức pha nước cam loại I

Nước cam loại I yêu cầu tỉ lệ bột cam là \( x_1 \) gram bột cam trên mỗi lít nước.

• Sử dụng \( x_1 \) gram bột cam pha với 1 lít nước lọc.
• Công thức: \( y_1 = x_1 \times V_1 \), trong đó \( V_1 \) là thể tích nước cần pha.
• Ví dụ: Nếu \( x_1 = 10 \) gram và \( V_1 = 2 \) lít, thì lượng bột cam cần dùng là \( y_1 = 10 \times 2 = 20 \) gram.

Công thức pha nước cam loại II

Nước cam loại II có tỉ lệ khác, yêu cầu \( x_2 \) gram bột cam trên mỗi lít nước.

• Sử dụng \( x_2 \) gram bột cam pha với 1 lít nước lọc.
• Công thức: \( y_2 = x_2 \times V_2 \), trong đó \( V_2 \) là thể tích nước cam loại II cần pha.
• Ví dụ: Nếu \( x_2 = 8 \) gram và \( V_2 = 3 \) lít, thì lượng bột cam cần dùng là \( y_2 = 8 \times 3 = 24 \) gram.

Giới hạn về lượng bột cam sử dụng

Tổng lượng bột cam sử dụng cho cả hai loại nước cam không vượt quá giới hạn đã cho. Giả sử giới hạn là \( T \) gram, ta có bất phương trình:

Trong đó:

• \( y_1 \): Lượng bột cam dùng cho nước cam loại I.
• \( y_2 \): Lượng bột cam dùng cho nước cam loại II.
• \( T \): Giới hạn tổng lượng bột cam có sẵn.

Ví dụ: Nếu \( T = 50 \) gram, thì tổng lượng bột cam sử dụng cho cả hai loại không được vượt quá 50 gram:

Để lập phương trình mô tả quá trình bạn Cúc pha hai loại nước cam, ta thực hiện theo các bước sau:

1. Gọi \(x\) là số lít nước cam loại I mà bạn Cúc muốn pha.
2. Gọi \(y\) là số lít nước cam loại II mà bạn Cúc muốn pha.
3. Số bột cam cần để pha chế:
• Nước cam loại I cần 30g bột cam cho mỗi lít, tức là \(30x\) (g).
• Nước cam loại II cần 20g bột cam cho mỗi lít, tức là \(20y\) (g).
4. Số bột cam tổng cộng cần sử dụng là \(30x + 20y\) (g).
5. Vì số bột cam bạn Cúc có không vượt quá 100g, ta có phương trình:


\[
30x + 20y \leq 100
\]

6. Rút gọn phương trình trên thành:


\[
3x + 2y \leq 10
\]

7. Vì số lít nước cam không thể âm, ta có thêm các điều kiện:
• \(x \geq 0\)
• \(y \geq 0\)

Như vậy, hệ phương trình bất phương trình mô tả số lít nước cam loại I và II mà bạn Cúc có thể pha được là:

• \(3x + 2y \leq 10\)
• \(x \geq 0\)
• \(y \geq 0\)

Đây là các phương trình và điều kiện cần thiết để giải quyết bài toán của bạn Cúc.

Để xác định miền nghiệm của bài toán, chúng ta sử dụng bất phương trình từ phần trước:

Bước đầu tiên là xác định đường thẳng tương ứng với bất phương trình:

Đường thẳng này cắt trục hoành và trục tung tại hai điểm:

• Điểm A (0; 5) khi \(x = 0\)
• Điểm B (10/3; 0) khi \(y = 0\)

Tiếp theo, ta sẽ xét dấu bất phương trình tại điểm gốc tọa độ \(O(0,0)\). Thay tọa độ điểm này vào bất phương trình:

Điểm \(O\) thỏa mãn bất phương trình, do đó miền nghiệm là nửa mặt phẳng phía dưới đường thẳng, bao gồm cả đường thẳng \(3x + 2y = 10\).

Để giải hệ bất phương trình và tìm miền nghiệm phù hợp, ta cần kết hợp với các điều kiện khác của bài toán (nếu có), ví dụ như điều kiện không âm:

• \(x \geq 0\)
• \(y \geq 0\)

Miền nghiệm cuối cùng sẽ là phần giao của các miền thỏa mãn từng bất phương trình.

Trong thực tế, bài toán pha hai loại nước cam có thể được áp dụng trong nhiều lĩnh vực khác nhau, đặc biệt là trong việc quản lý nguyên liệu và tối ưu hóa quy trình sản xuất. Một ví dụ cụ thể là khi cần pha chế hai loại nước cam với hàm lượng bột cam khác nhau, nhưng bị giới hạn về tổng lượng bột cam sử dụng.

Giả sử, để pha chế:

• Nước cam loại I: cần 30g bột cam để pha mỗi lít nước cam.
• Nước cam loại II: cần 20g bột cam để pha mỗi lít nước cam.

Như vậy, bài toán có thể được thiết lập thành một hệ bất phương trình tuyến tính để tìm ra cách phân chia hợp lý lượng nước cam loại I và II sao cho tổng lượng bột cam không vượt quá giới hạn.

Cho \( x \) là số lít nước cam loại I và \( y \) là số lít nước cam loại II, ta có:

Giải hệ bất phương trình này sẽ giúp tìm ra miền nghiệm, từ đó xác định được các giá trị phù hợp cho \( x \) và \( y \). Phương pháp này có thể áp dụng rộng rãi trong các quy trình sản xuất thực phẩm, đồ uống, hoặc bất kỳ quá trình nào yêu cầu tối ưu hóa sử dụng nguyên liệu.

Trong miền nghiệm đã tìm ra, ta có thể lựa chọn các giá trị \( x \) và \( y \) sao cho phù hợp với yêu cầu sản xuất thực tế. Ví dụ, nếu muốn pha 2 lít nước cam loại I, ta có thể tính lượng nước cam loại II tối đa có thể pha là:

Do đó, ta có thể pha tối đa 2 lít nước cam loại II.

Qua bài toán pha hai loại nước cam, ta có thể thấy rằng việc áp dụng kiến thức toán học vào thực tế là rất hữu ích. Cụ thể, thông qua bài toán, bạn Cúc có thể tính toán chính xác lượng bột cam cần dùng cho hai loại nước cam, đảm bảo không vượt quá lượng bột có sẵn. Phương pháp này không chỉ giúp tối ưu hóa việc sử dụng nguyên liệu mà còn giúp quản lý tài nguyên hiệu quả trong cuộc sống hàng ngày.

Bài toán này được mô tả bằng hệ bất phương trình:

• \(x \geq 0\) (số lít nước cam loại I)
• \(y \geq 0\) (số lít nước cam loại II)
• \(3x + 2y \leq 10\) (hạn chế về lượng bột cam)

Giải hệ bất phương trình này trên mặt phẳng tọa độ giúp bạn Cúc tìm ra miền nghiệm, từ đó xác định được những phương án pha chế hợp lý nhất. Đây là một minh chứng điển hình về việc vận dụng toán học vào giải quyết các bài toán đời thường một cách khoa học và chính xác.