Một tàu đánh cá xuất phát từ cảng A: Hành trình và bài học quan trọng

Hành trình của tàu đánh cá xuất phát từ cảng A có thể được mô tả qua các bước sau:

1. Xuất phát từ cảng A: Tàu đánh cá rời cảng A, ban đầu di chuyển về hướng Đông Nam với vận tốc không đổi. Giả định rằng tàu đi theo góc \(70^\circ\) về hướng Đông Nam, điều này sẽ ảnh hưởng đến tính toán quãng đường và vị trí của tàu trong các bước tiếp theo.
2. Quãng đường đi được trong 90 phút: Với vận tốc di chuyển ban đầu là 70 km/h, sau 90 phút (tức 1.5 giờ), tàu đã đi được quãng đường: \[ AB = 70 \times 1.5 = 105 \, \text{km} \]
3. Sự cố và trôi tự do: Sau khi đi được 105 km, tàu gặp sự cố và bắt đầu trôi theo hướng Nam với vận tốc 8 km/h. Tàu trôi trong thời gian 2 giờ, tạo ra quãng đường: \[ BC = 8 \times 2 = 16 \, \text{km} \]
4. Tính toán khoảng cách từ cảng A đến vị trí đích: Sử dụng định lý cosin để tính khoảng cách từ cảng A đến nơi tàu neo đậu: \[ AC^2 = AB^2 + BC^2 - 2 \times AB \times BC \times \cos(70^\circ) \] \[ AC \approx 111.5 \, \text{km} \]
5. Hướng di chuyển từ cảng A đến đích: Từ đó, ta có thể xác định hướng từ cảng A đến vị trí đích là khoảng \(70^\circ\) về phía Đông Nam, dựa trên vị trí ban đầu và góc di chuyển.

Qua hành trình này, chúng ta có thể thấy được sự phức tạp trong việc điều hướng tàu trên biển khi gặp phải sự cố. Tính toán kỹ lưỡng quãng đường và góc di chuyển giúp đảm bảo tàu đến đích an toàn.

Trong quá trình di chuyển của tàu đánh cá, chúng ta có thể tính toán chính xác quãng đường và góc di chuyển thông qua các công thức lượng giác và hệ thức trong tam giác. Dưới đây là các bước phân tích chi tiết:

1. Tính toán quãng đường đi được: Ban đầu, tàu di chuyển từ cảng A theo hướng Đông Nam với vận tốc 70 km/h trong thời gian 90 phút. Quãng đường đi được là: \[ AB = 70 \times 1.5 = 105 \, \text{km} \] Đây là quãng đường thẳng tính từ cảng A đến vị trí B, nơi mà tàu gặp sự cố.
2. Quá trình trôi tự do: Sau sự cố, tàu bắt đầu trôi về phía Nam với vận tốc 8 km/h trong thời gian 2 giờ. Quãng đường trôi tự do của tàu là: \[ BC = 8 \times 2 = 16 \, \text{km} \]
3. Tính góc giữa hai hướng di chuyển: Góc giữa hướng di chuyển ban đầu và hướng trôi tự do được giả định là \(110^\circ\). Đây là góc giữa hai phương vị Đông Nam và Nam, giúp ta tính được khoảng cách giữa hai vị trí.
4. Khoảng cách từ cảng A đến điểm neo đậu: Sử dụng định lý cosin, ta có thể tính được khoảng cách AC từ cảng A đến vị trí neo đậu cuối cùng của tàu: \[ AC^2 = AB^2 + BC^2 - 2 \times AB \times BC \times \cos(110^\circ) \] Thay số vào, ta được: \[ AC \approx \sqrt{105^2 + 16^2 - 2 \times 105 \times 16 \times \cos(110^\circ)} \approx 111.49 \, \text{km} \]
5. Phân tích góc di chuyển từ cảng A đến điểm neo đậu: Để xác định hướng chính xác từ cảng A đến điểm neo đậu, chúng ta sử dụng hệ thức lượng giác trong tam giác và tìm ra rằng tàu di chuyển theo góc \(70^\circ\) so với phương Đông, tạo ra hành trình phức tạp và thú vị trên biển.

Phân tích quãng đường và góc di chuyển giúp ta có cái nhìn chi tiết về hành trình của tàu, cũng như cách áp dụng toán học vào thực tiễn hàng hải.

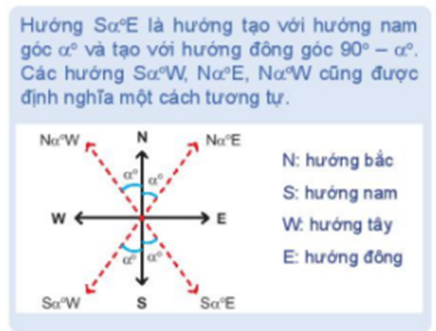
Trong bài toán về hành trình của một tàu đánh cá xuất phát từ cảng A, vận tốc và các góc di chuyển đóng vai trò quan trọng trong việc xác định quãng đường và vị trí của tàu. Cụ thể, tàu di chuyển theo hướng \( S70^{\circ}E \) với vận tốc 70 km/h. Sau 90 phút di chuyển, tàu gặp sự cố và trôi theo hướng Nam với vận tốc 8 km/h trong 2 giờ.

Quá trình này đòi hỏi sử dụng các kiến thức về vận tốc và góc trong hệ thức lượng giác để xác định khoảng cách từ điểm xuất phát đến vị trí hiện tại của tàu. Dưới đây là các bước chính để tính toán:

1. Tính quãng đường đầu tiên: Tàu di chuyển theo hướng \( S70^{\circ}E \) trong 90 phút, tương đương với 1.5 giờ. Quãng đường di chuyển được tính bằng công thức: \[ d_1 = v_1 \times t_1 = 70 \, \text{km/h} \times 1.5 \, \text{h} = 105 \, \text{km}. \]
2. Tính quãng đường tàu trôi: Khi động cơ ngừng hoạt động, tàu trôi theo hướng Nam với vận tốc 8 km/h trong 2 giờ. Quãng đường tàu trôi là: \[ d_2 = v_2 \times t_2 = 8 \, \text{km/h} \times 2 \, \text{h} = 16 \, \text{km}. \]
3. Sử dụng định lý cos để tính khoảng cách: Khoảng cách tổng cộng từ điểm xuất phát đến nơi tàu dừng lại có thể tính bằng định lý cos: \[ AC^2 = AB^2 + BC^2 - 2 \times AB \times BC \times \cos(110^\circ). \] Trong đó, \( AB = 105 \, \text{km} \), \( BC = 16 \, \text{km} \), và góc giữa hai đoạn là 110 độ (do tàu di chuyển theo hướng S70E và sau đó trôi theo hướng Nam).

Việc sử dụng công thức vận tốc và các công cụ toán học như định lý cos giúp dễ dàng xác định khoảng cách và vị trí của tàu trong bài toán này.