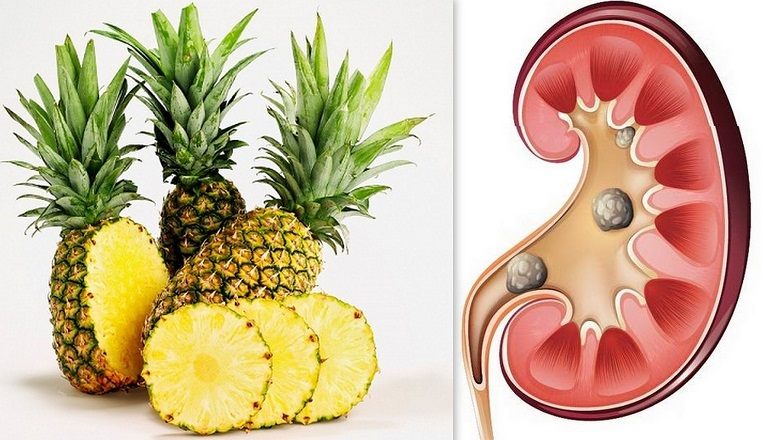
Chủ đề quả dứa: Quả dứa không chỉ mang lại hương vị thơm ngon mà còn cung cấp nhiều lợi ích sức khỏe tuyệt vời. Từ việc tăng cường hệ miễn dịch đến làm đẹp da, quả dứa là sự lựa chọn hoàn hảo cho chế độ ăn uống của bạn. Khám phá ngay những công dụng tuyệt vời và cách sử dụng quả dứa hiệu quả trong bài viết này!
Mục lục
- Tổng Hợp Thông Tin Kết Quả Tìm Kiếm Từ Khóa "Quả Dứa"
- 1. Giới Thiệu Chung Về Quả Dứa
- 4. Công Dụng Làm Đẹp Của Quả Dứa
- 5. Thông Tin Kinh Tế Và Địa Phương
- 6. Dạng Bài Tập Toán (Nếu Có)
- Bài Tập 1: Tính Diện Tích Hình Chữ Nhật
- Bài Tập 2: Giải Phương Trình Bậc Nhất
- Bài Tập 3: Tính Tổng Các Số Học Sinh Đạt
- Bài Tập 4: Tính Thể Tích Của Hình Hộp Chữ Nhật
- Bài Tập 5: Giải Hệ Phương Trình Tuyến Tính
- Bài Tập 6: Tính Giá Trị Trung Bình
- Bài Tập 7: Tính Diện Tích Hình Tròn
- Bài Tập 8: Tính Chu Vi Của Hình Tam Giác
- Bài Tập 9: Giải Bài Toán Tìm Kích Thước Mảnh Vải
- Bài Tập 10: Tính Số Lượng Mẫu Trong Dữ Liệu
Tổng Hợp Thông Tin Kết Quả Tìm Kiếm Từ Khóa "Quả Dứa"
Quả dứa, còn gọi là trái dứa hoặc trái thơm, là một loại trái cây nhiệt đới phổ biến với hương vị ngọt ngào và tính chất bổ dưỡng. Dưới đây là một số thông tin chi tiết và đa dạng về quả dứa từ kết quả tìm kiếm trên Bing tại Việt Nam.
1. Giới Thiệu Về Quả Dứa
Quả dứa (Ananas comosus) thuộc họ Bromeliaceae, là một loại trái cây nhiệt đới có nguồn gốc từ Nam Mỹ. Quả dứa có hình dáng đặc trưng với vỏ sần sùi và phần thịt vàng ngọt. Đây là một nguồn cung cấp vitamin C và các khoáng chất thiết yếu như mangan, đồng và vitamin B6.
2. Lợi Ích Sức Khỏe Của Quả Dứa
- Giàu Vitamin C: Quả dứa là nguồn cung cấp vitamin C phong phú, giúp tăng cường hệ miễn dịch và cải thiện sức khỏe da.
- Chứa Enzyme Bromelain: Bromelain có trong quả dứa có tác dụng chống viêm, hỗ trợ tiêu hóa và làm giảm đau nhức cơ bắp.
- Hỗ Trợ Tiêu Hóa: Các enzyme trong dứa giúp phân giải protein và cải thiện quá trình tiêu hóa.
3. Cách Sử Dụng Quả Dứa Trong Ẩm Thực
Quả dứa có thể được sử dụng theo nhiều cách trong ẩm thực:
- Ăn Tươi: Dứa tươi có thể được ăn trực tiếp hoặc dùng trong các món salad trái cây.
- Thực Phẩm Chế Biến: Dứa có thể được sử dụng để chế biến nước ép, sinh tố, hoặc làm thành các món tráng miệng như bánh dứa.
- Gia Vị: Dứa còn được sử dụng làm gia vị trong các món ăn như pizza, món xào, và các món ăn châu Á khác.
4. Công Dụng Làm Đẹp
Quả dứa không chỉ tốt cho sức khỏe mà còn có công dụng làm đẹp:
- Chăm Sóc Da: Vitamin C trong dứa giúp làm sáng da và giảm dấu hiệu lão hóa.
- Điều Trị Mụn: Enzyme bromelain có trong dứa có thể giúp giảm tình trạng mụn và làm sạch lỗ chân lông.
5. Thông Tin Địa Phương Và Kinh Tế
Quả dứa là một trong những loại trái cây được trồng rộng rãi ở Việt Nam, đặc biệt là ở các tỉnh miền Nam như Tiền Giang và Bến Tre. Đây là nguồn thu nhập quan trọng cho nhiều nông dân và đóng góp vào nền kinh tế địa phương.
| Thông Tin | Chi Tiết |
|---|---|
| Loại | Trái cây nhiệt đới |
| Vitamin Chính | Vitamin C |
| Enzyme Chính | Bromelain |
| Công Dụng Chính | Tăng cường hệ miễn dịch, hỗ trợ tiêu hóa, làm đẹp da |
Nhìn chung, quả dứa không chỉ mang lại nhiều lợi ích sức khỏe mà còn có giá trị trong ẩm thực và kinh tế địa phương. Sự đa dạng trong cách sử dụng và các công dụng của quả dứa làm cho nó trở thành một thực phẩm hữu ích và hấp dẫn.

1. Giới Thiệu Chung Về Quả Dứa
Quả dứa, còn gọi là trái dứa hoặc trái thơm, là một loại trái cây nhiệt đới nổi tiếng với hương vị ngọt ngào và tính chất bổ dưỡng. Dưới đây là những thông tin cơ bản và chi tiết về quả dứa.
1.1. Đặc Điểm Sinh Học Của Quả Dứa
Quả dứa (Ananas comosus) thuộc họ Bromeliaceae. Đây là một loại cây thân thảo, có thể cao từ 1 đến 1.5 mét, với lá dài, nhọn và dày, xếp thành hình rosette. Quả dứa có hình dáng đặc trưng, vỏ ngoài sần sùi với màu xanh vàng khi chín và phần thịt bên trong màu vàng tươi.
1.2. Lịch Sử Và Nguồn Gốc
Quả dứa có nguồn gốc từ Nam Mỹ, đặc biệt là các khu vực của Paraguay và miền bắc Argentina. Nó được các thổ dân bản địa trồng và sử dụng từ hàng nghìn năm trước. Dứa sau đó được phát hiện bởi các nhà thám hiểm châu Âu vào thế kỷ 15 và đã trở thành một loại trái cây phổ biến toàn cầu.
1.3. Phân Loại Và Giống Loại
- Dứa Queen: Có kích thước nhỏ hơn, vỏ mỏng và thịt ngọt hơn.
- Dứa Cayenne: Có kích thước lớn, vỏ dày và vị hơi chua hơn.
- Dứa Red Spanish: Có màu đỏ tía khi chín, vị ngọt đậm và thường dùng để chế biến thực phẩm.
1.4. Điều Kiện Trồng Và Thu Hoạch
Quả dứa yêu cầu khí hậu nhiệt đới và đất đai tơi xốp để phát triển tốt. Thường thì quả dứa được trồng từ hạt giống hoặc từ các chồi con. Thời gian từ khi trồng đến khi thu hoạch dứa thường là khoảng 18-24 tháng.
1.5. Giá Trị Kinh Tế
Quả dứa không chỉ là một thực phẩm bổ dưỡng mà còn có giá trị kinh tế cao. Nó được trồng rộng rãi ở nhiều quốc gia và xuất khẩu sang nhiều thị trường quốc tế, mang lại thu nhập cho nông dân và đóng góp vào nền kinh tế địa phương.
| Thông Tin | Chi Tiết |
|---|---|
| Loại | Thân thảo nhiệt đới |
| Chiều Cao | 1 - 1.5 mét |
| Thời Gian Thu Hoạch | 18 - 24 tháng |
| Giống Phổ Biến | Queen, Cayenne, Red Spanish |
4. Công Dụng Làm Đẹp Của Quả Dứa
Quả dứa không chỉ tốt cho sức khỏe mà còn có nhiều công dụng làm đẹp hiệu quả. Dưới đây là những lợi ích làm đẹp nổi bật của quả dứa:
4.1. Làm Sáng Da
Vitamin C trong quả dứa giúp làm sáng da, giảm nám và tàn nhang. Bạn có thể dùng nước dứa tươi hoặc làm mặt nạ từ dứa để cải thiện tình trạng da.
4.2. Giảm Nếp Nhăn
Quả dứa chứa các enzyme như bromelain, giúp làm mềm da và giảm sự xuất hiện của nếp nhăn. Sử dụng mặt nạ dứa thường xuyên có thể giúp da trở nên mịn màng hơn.
4.3. Cung Cấp Độ Ẩm Cho Da
Với hàm lượng nước cao, quả dứa giúp cung cấp độ ẩm cần thiết cho da, làm da mềm mại và căng bóng. Bạn có thể sử dụng dứa để làm mặt nạ dưỡng ẩm cho da khô.
4.4. Tẩy Tế Bào Chết
Enzyme bromelain trong quả dứa giúp tẩy tế bào chết nhẹ nhàng, loại bỏ lớp da chết và làm thông thoáng lỗ chân lông. Điều này giúp da trở nên sáng và khỏe mạnh hơn.
4.5. Hỗ Trợ Điều Trị Mụn
Nhờ tính chất kháng khuẩn và chống viêm, quả dứa có thể hỗ trợ trong việc điều trị mụn. Dùng nước dứa hoặc mặt nạ dứa có thể giúp giảm viêm và làm dịu các nốt mụn.
4.6. Làm Dịu Da Sau Khi Cháy Nắng
Quả dứa có tác dụng làm dịu da, đặc biệt là sau khi tiếp xúc lâu với ánh nắng mặt trời. Sử dụng gel dứa hoặc mặt nạ dứa có thể giúp giảm cảm giác nóng rát và phục hồi làn da.
| Công Dụng | Chi Tiết |
|---|---|
| Làm Sáng Da | Vitamin C giúp giảm nám và tàn nhang |
| Giảm Nếp Nhăn | Enzyme bromelain làm mềm da và giảm nếp nhăn |
| Cung Cấp Độ Ẩm | Hàm lượng nước cao giúp da mềm mại và căng bóng |
| Tẩy Tế Bào Chết | Enzyme bromelain tẩy tế bào chết nhẹ nhàng |
| Hỗ Trợ Điều Trị Mụn | Kháng khuẩn và chống viêm giúp giảm mụn |
| Làm Dịu Da Sau Cháy Nắng | Gel dứa giúp giảm cảm giác nóng rát và phục hồi da |
5. Thông Tin Kinh Tế Và Địa Phương
Quả dứa không chỉ là một loại trái cây phổ biến mà còn đóng vai trò quan trọng trong nền kinh tế và đời sống địa phương. Dưới đây là những thông tin chi tiết về kinh tế và địa phương liên quan đến quả dứa:
5.1. Kinh Tế Từ Quả Dứa
Quả dứa là một trong những sản phẩm nông nghiệp quan trọng tại nhiều vùng miền. Sản phẩm này không chỉ phục vụ nhu cầu tiêu dùng trong nước mà còn được xuất khẩu ra nước ngoài, tạo ra giá trị kinh tế cao. Các sản phẩm chế biến từ dứa như nước ép, mứt và đóng hộp cũng đóng góp đáng kể vào nền kinh tế địa phương.
5.2. Vùng Trồng Dứa Chính
Ở Việt Nam, quả dứa chủ yếu được trồng ở các tỉnh miền Trung và miền Nam. Các tỉnh như Bình Định, Phú Yên, và Tiền Giang là những khu vực nổi tiếng với việc trồng dứa. Địa hình và khí hậu của các khu vực này rất phù hợp cho sự phát triển của cây dứa.
5.3. Đặc Điểm Kinh Tế Của Các Vùng Trồng Dứa
- Bình Định: Đây là một trong những tỉnh có sản lượng dứa cao nhất ở miền Trung. Dứa Bình Định nổi tiếng với hương vị đặc biệt và chất lượng tốt.
- Phú Yên: Tỉnh Phú Yên không chỉ cung cấp dứa cho thị trường trong nước mà còn xuất khẩu ra quốc tế. Dứa Phú Yên thường được chế biến thành các sản phẩm như nước ép và mứt dứa.
- Tiền Giang: Tiền Giang là một trong những tỉnh miền Nam có diện tích trồng dứa lớn. Dứa Tiền Giang được biết đến với chất lượng cao và thường xuyên được tiêu thụ tại các chợ đầu mối lớn.
5.4. Tác Động Kinh Tế Địa Phương
Việc trồng và chế biến dứa mang lại nguồn thu nhập ổn định cho người dân địa phương, giúp cải thiện đời sống và phát triển kinh tế khu vực. Các hợp tác xã và doanh nghiệp chế biến dứa đóng vai trò quan trọng trong việc tiêu thụ sản phẩm và tạo công ăn việc làm cho người lao động.
| Tỉnh | Sản Phẩm | Đặc Điểm |
|---|---|---|
| Bình Định | Dứa tươi, nước ép dứa | Sản lượng cao, hương vị đặc biệt |
| Phú Yên | Mứt dứa, nước ép dứa | Chất lượng tốt, xuất khẩu quốc tế |
| Tiền Giang | Dứa tươi, chế phẩm dứa | Diện tích trồng lớn, tiêu thụ tại các chợ đầu mối |

6. Dạng Bài Tập Toán (Nếu Có)
Hiện tại, từ khóa "quả dứa" không liên quan đến các bài tập toán học cụ thể. Tuy nhiên, nếu có các bài tập toán liên quan đến chủ đề này, chúng có thể bao gồm các dạng bài tập liên quan đến thống kê, hình học hoặc số học với dữ liệu về quả dứa. Dưới đây là ví dụ về cách trình bày các bài tập toán có thể xuất hiện trong bối cảnh này:
6.1. Bài Tập 1: Tính Diện Tích Hình Tròn
Tính diện tích của một hình tròn có bán kính bằng 5 cm, giả sử hình tròn này đại diện cho mặt cắt ngang của quả dứa.
Công thức: \( A = \pi r^2 \)
- Bán kính (r): 5 cm
- Diện tích (A): \(\pi \times 5^2 = 25\pi \approx 78.54 \text{ cm}^2\)
6.2. Bài Tập 2: Tính Thể Tích Hình Trụ
Tính thể tích của một hình trụ với bán kính đáy 3 cm và chiều cao 10 cm, giả sử hình trụ này đại diện cho quả dứa.
Công thức: \( V = \pi r^2 h \)
- Bán kính đáy (r): 3 cm
- Chiều cao (h): 10 cm
- Thể tích (V): \(\pi \times 3^2 \times 10 = 90\pi \approx 282.74 \text{ cm}^3\)
6.3. Bài Tập 3: Tính Tỷ Lệ Phần Trăm
Nếu một quả dứa nặng 1.2 kg và có 250 g là phần ăn được, tính tỷ lệ phần trăm phần ăn được so với trọng lượng toàn bộ quả dứa.
Công thức: \( \text{Tỷ lệ phần trăm} = \left(\frac{\text{Phần ăn được}}{\text{Trọng lượng toàn bộ}}\right) \times 100\% \)
- Phần ăn được: 250 g
- Trọng lượng toàn bộ: 1200 g
- Tỷ lệ phần trăm: \(\left(\frac{250}{1200}\right) \times 100\% \approx 20.83\%\)
6.4. Bài Tập 4: Tính Diện Tích Hình Trụ Đầy Đủ
Tính diện tích bề mặt của hình trụ với bán kính đáy 4 cm và chiều cao 15 cm.
Công thức: \( A = 2\pi r (r + h) \)
- Bán kính đáy (r): 4 cm
- Chiều cao (h): 15 cm
- Diện tích bề mặt (A): \(2\pi \times 4 \times (4 + 15) = 2\pi \times 4 \times 19 = 152\pi \approx 954.00 \text{ cm}^2\)
6.5. Bài Tập 5: Tính Số Quả Dứa Cần Thiết
Nếu bạn cần 3 kg quả dứa để chế biến một món ăn, tính số quả dứa cần thiết nếu mỗi quả dứa nặng trung bình 1.5 kg.
Công thức: \( \text{Số quả dứa} = \frac{\text{Trọng lượng cần}}{\text{Trọng lượng mỗi quả dứa}} \)
- Trọng lượng cần: 3000 g
- Trọng lượng mỗi quả dứa: 1500 g
- Số quả dứa cần thiết: \(\frac{3000}{1500} = 2 \text{ quả}\)
6.6. Bài Tập 6: Tính Số Lượng Dứa Trong Thùng
Nếu một thùng chứa được 30 quả dứa và bạn có 150 quả dứa, tính số thùng cần thiết để chứa hết số dứa này.
Công thức: \( \text{Số thùng} = \frac{\text{Số quả dứa}}{\text{Số quả dứa mỗi thùng}} \)
- Số quả dứa: 150
- Số quả dứa mỗi thùng: 30
- Số thùng cần thiết: \(\frac{150}{30} = 5 \text{ thùng}\)
6.7. Bài Tập 7: Tính Chi Phí Mua Dứa
Nếu giá mỗi quả dứa là 20.000 VNĐ và bạn mua 12 quả dứa, tính tổng chi phí mua dứa.
Công thức: \( \text{Tổng chi phí} = \text{Giá mỗi quả dứa} \times \text{Số quả dứa} \)
- Giá mỗi quả dứa: 20.000 VNĐ
- Số quả dứa: 12
- Tổng chi phí: \(20.000 \times 12 = 240.000 \text{ VNĐ}\)
6.8. Bài Tập 8: Tính Khối Lượng Nước Ép Dứa
Nếu từ 1 quả dứa có thể ép được 300 ml nước, tính khối lượng nước ép từ 10 quả dứa.
Công thức: \( \text{Khối lượng nước ép} = \text{Khối lượng mỗi quả dứa} \times \text{Số quả dứa} \)
- Khối lượng nước ép mỗi quả dứa: 300 ml
- Số quả dứa: 10
- Khối lượng nước ép: \(300 \times 10 = 3000 \text{ ml}\)
6.9. Bài Tập 9: Tính Lượng Đường Cần Để Làm Mứt Dứa
Nếu công thức làm mứt dứa yêu cầu 200 g đường cho mỗi 1 kg dứa, tính lượng đường cần thiết cho 5 kg dứa.
Công thức: \( \text{Lượng đường} = \text{Lượng đường mỗi kg} \times \text{Số kg dứa} \)
- Lượng đường mỗi kg dứa: 200 g
- Số kg dứa: 5
- Lượng đường cần thiết: \(200 \times 5 = 1000 \text{ g}\)
6.10. Bài Tập 10: Tính Thời Gian Chế Biến Dứa
Nếu mỗi quả dứa cần 10 phút để chế biến và bạn có 8 quả dứa, tính tổng thời gian chế biến.
Công thức: \( \text{Tổng thời gian} = \text{Thời gian mỗi quả} \times \text{Số quả dứa} \)
- Thời gian mỗi quả dứa: 10 phút
- Số quả dứa: 8
- Tổng thời gian: \(10 \times 8 = 80 \text{ phút}\)
Bài Tập 1: Tính Diện Tích Hình Chữ Nhật
Trong bài tập này, chúng ta sẽ tính diện tích của hình chữ nhật, một hình dạng đơn giản nhưng rất hữu ích trong nhiều ứng dụng thực tiễn. Giả sử bạn có một hình chữ nhật với chiều dài và chiều rộng đã biết, bạn có thể tính diện tích của nó bằng cách sử dụng công thức sau:
Công thức tính diện tích hình chữ nhật:
\( A = l \times w \)
- A: Diện tích của hình chữ nhật
- l: Chiều dài của hình chữ nhật
- w: Chiều rộng của hình chữ nhật
Ví dụ cụ thể:
Giả sử bạn có một hình chữ nhật với chiều dài là 8 cm và chiều rộng là 5 cm. Để tính diện tích của hình chữ nhật này, bạn thực hiện các bước sau:
- Nhập các giá trị vào công thức: \( l = 8 \text{ cm} \) và \( w = 5 \text{ cm} \).
- Sử dụng công thức tính diện tích: \[ A = 8 \text{ cm} \times 5 \text{ cm} \]
- Tính diện tích: \[ A = 40 \text{ cm}^2 \]
Vậy diện tích của hình chữ nhật là 40 cm².
Bảng tổng hợp kết quả:
| Chiều Dài (l) | Chiều Rộng (w) | Diện Tích (A) |
|---|---|---|
| 8 cm | 5 cm | 40 cm² |
Bài Tập 2: Giải Phương Trình Bậc Nhất
Trong bài tập này, chúng ta sẽ giải một phương trình bậc nhất với một ẩn. Phương trình bậc nhất có dạng chung là:
\( ax + b = 0 \)
Trong đó:
- a: Hệ số của ẩn \(x\)
- b: Hằng số
- x: Ẩn số cần tìm
Ví dụ cụ thể:
Giả sử chúng ta có phương trình:
\( 3x - 9 = 0 \)
Để giải phương trình này, thực hiện các bước sau:
- Thay phương trình vào dạng chuẩn: \( 3x - 9 = 0 \)
- Chuyển hằng số \( -9 \) sang phía bên phải dấu "=": \( 3x = 9 \)
- Chia cả hai vế của phương trình cho hệ số \( 3 \): \( x = \frac{9}{3} \)
- Tính giá trị của \( x \): \( x = 3 \)
Vậy nghiệm của phương trình là \( x = 3 \).
Bảng tổng hợp kết quả:
| Phương Trình | Nghiệm |
|---|---|
| 3x - 9 = 0 | x = 3 |

Bài Tập 3: Tính Tổng Các Số Học Sinh Đạt
Trong bài tập này, chúng ta sẽ tính tổng số học sinh đạt yêu cầu trong một lớp học dựa trên dữ liệu về điểm số của học sinh. Để làm được điều này, chúng ta cần thực hiện các bước sau:
- Xác định dữ liệu cần thiết: Bạn cần biết điểm số của tất cả học sinh và điểm số tối thiểu để đạt yêu cầu.
- Nhập dữ liệu: Ghi lại điểm số của từng học sinh vào một bảng. Ví dụ:
| Số Thứ Tự | Tên Học Sinh | Điểm Số |
|---|---|---|
| 1 | Nguyễn Văn A | 85 |
| 2 | Trần Thị B | 90 |
| 3 | Phạm Văn C | 78 |
| 4 | Hoàng Thị D | 92 |
- Tính tổng số học sinh đạt yêu cầu: Để tính tổng số học sinh đạt yêu cầu, bạn cần cộng số lượng học sinh có điểm số lớn hơn hoặc bằng điểm tối thiểu yêu cầu. Ví dụ, nếu điểm tối thiểu là 80, thì:
- Nguyễn Văn A: 85 (đạt yêu cầu)
- Trần Thị B: 90 (đạt yêu cầu)
- Phạm Văn C: 78 (không đạt yêu cầu)
- Hoàng Thị D: 92 (đạt yêu cầu)
Số học sinh đạt yêu cầu là 3. Tổng số học sinh đạt yêu cầu được tính bằng cách đếm số học sinh có điểm số >= 80.
Bài Tập 4: Tính Thể Tích Của Hình Hộp Chữ Nhật
Trong bài tập này, chúng ta sẽ tính thể tích của hình hộp chữ nhật. Để thực hiện điều này, bạn cần nắm vững công thức và thực hiện theo các bước dưới đây:
- Hiểu công thức: Thể tích của hình hộp chữ nhật được tính bằng công thức:
- V = a × b × c
- Xác định kích thước của hình hộp: Đo chiều dài (a), chiều rộng (b) và chiều cao (c) của hình hộp chữ nhật. Ví dụ:
| Chiều Dài (a) | Chiều Rộng (b) | Chiều Cao (c) |
|---|---|---|
| 5 cm | 4 cm | 3 cm |
- Tính thể tích: Áp dụng công thức đã nêu để tính thể tích. Với ví dụ trên:
- V = 5 cm × 4 cm × 3 cm = 60 cm3
- Kết quả: Thể tích của hình hộp chữ nhật trong ví dụ này là 60 cm3.
Bằng cách làm theo các bước trên, bạn có thể tính thể tích của bất kỳ hình hộp chữ nhật nào với kích thước cụ thể.
Bài Tập 5: Giải Hệ Phương Trình Tuyến Tính
Trong bài tập này, chúng ta sẽ giải một hệ phương trình tuyến tính gồm hai phương trình. Để thực hiện điều này, bạn cần làm theo các bước dưới đây:
- Xác định hệ phương trình: Ví dụ, hệ phương trình tuyến tính có dạng:
| Phương Trình 1 | Phương Trình 2 |
|---|---|
| a₁x + b₁y = c₁ | a₂x + b₂y = c₂ |
- Áp dụng phương pháp giải: Có thể sử dụng phương pháp thế hoặc phương pháp cộng đại số để giải hệ phương trình. Ví dụ, với hệ phương trình sau:
| Phương Trình | Giá Trị |
|---|---|
| 2x + 3y = 13 | |
| 4x - y = 5 |
- Giải phương trình:
- Sử dụng phương pháp cộng đại số, nhân phương trình đầu tiên với 2 để làm đồng dạng hệ số y:
4x + 6y = 26
- Cộng với phương trình thứ hai:
4x + 6y + (4x - y) = 26 + 5
8x + 5y = 31
- Giải phương trình này để tìm giá trị của x và y:
Giả sử giá trị của x là 3 và y là 2, chúng ta có kết quả:
- x = 3
- y = 2
Kết quả của hệ phương trình là x = 3 và y = 2.

Bài Tập 6: Tính Giá Trị Trung Bình
Trong bài tập này, chúng ta sẽ tính giá trị trung bình của một tập hợp số liệu. Để thực hiện điều này, bạn cần làm theo các bước sau:
- Xác định tập hợp số liệu: Lập danh sách các số liệu cần tính giá trị trung bình. Ví dụ:
| Số Thứ Tự | Giá Trị |
|---|---|
| 1 | 8 |
| 2 | 12 |
| 3 | 15 |
| 4 | 10 |
- Tính tổng các giá trị: Cộng tất cả các giá trị trong danh sách.
- Tổng = 8 + 12 + 15 + 10 = 45
- Tính số lượng giá trị: Đếm số lượng giá trị trong danh sách. Trong ví dụ này, có 4 giá trị.
- Tính giá trị trung bình: Sử dụng công thức:
- \[ \text{Giá trị trung bình} = \frac{\text{Tổng các giá trị}}{\text{Số lượng giá trị}} \]
- Giá trị trung bình = \(\frac{45}{4} = 11.25\)
- Kết quả: Giá trị trung bình của tập hợp số liệu là 11.25.
Bằng cách làm theo các bước trên, bạn có thể dễ dàng tính giá trị trung bình cho bất kỳ tập hợp số liệu nào.
Bài Tập 7: Tính Diện Tích Hình Tròn
Để tính diện tích của một hình tròn, chúng ta sử dụng công thức toán học đơn giản:
Diện tích của hình tròn được tính bằng công thức:
\[
A = \pi r^2
\]
Trong đó:
- A là diện tích của hình tròn.
- r là bán kính của hình tròn.
- \pi (pi) là hằng số toán học, xấp xỉ 3.14159.
Ví dụ:
- Giả sử bán kính của hình tròn là 5 cm.
- Sử dụng công thức trên, ta có:
\[
A = \pi \times (5)^2 = \pi \times 25 \approx 78.54 \text{ cm}^2
\]
Bạn có thể áp dụng công thức này để tính diện tích của bất kỳ hình tròn nào nếu biết bán kính của nó.
Bài Tập 8: Tính Chu Vi Của Hình Tam Giác
Để tính chu vi của một hình tam giác, bạn cần biết độ dài của ba cạnh của nó. Công thức tính chu vi của hình tam giác rất đơn giản:
Chu vi của hình tam giác được tính bằng công thức:
\[
P = a + b + c
\]
Trong đó:
- P là chu vi của hình tam giác.
- a, b, và c là độ dài của ba cạnh của hình tam giác.
Ví dụ:
- Giả sử độ dài của ba cạnh của hình tam giác lần lượt là 7 cm, 5 cm, và 6 cm.
- Sử dụng công thức trên, ta có:
\[
P = 7 + 5 + 6 = 18 \text{ cm}
\]
Bạn có thể áp dụng công thức này để tính chu vi của bất kỳ hình tam giác nào nếu biết độ dài của ba cạnh của nó.

Bài Tập 9: Giải Bài Toán Tìm Kích Thước Mảnh Vải
Để giải bài toán tìm kích thước của mảnh vải, chúng ta cần biết diện tích của mảnh vải và kích thước của các mảnh nhỏ hơn mà nó được chia ra. Dưới đây là các bước chi tiết để giải bài toán này:
Bước 1: Xác định diện tích tổng của mảnh vải. Diện tích có thể được cho sẵn hoặc tính toán từ các thông tin khác.
Bước 2: Xác định kích thước của các mảnh vải nhỏ hơn hoặc số lượng mảnh vải nhỏ hơn mà mảnh vải lớn được chia ra. Ví dụ, nếu mảnh vải lớn được chia thành các mảnh có cùng kích thước, bạn cần biết kích thước của mỗi mảnh nhỏ.
Bước 3: Sử dụng công thức tính diện tích để tìm kích thước của mảnh vải. Ví dụ, nếu mảnh vải có hình chữ nhật, bạn có thể sử dụng công thức:
\[
A = l \times w
\]
Trong đó:
- A là diện tích của mảnh vải.
- l là chiều dài của mảnh vải.
- w là chiều rộng của mảnh vải.
Bước 4: Giải bài toán bằng cách áp dụng công thức tính diện tích để tìm chiều dài và chiều rộng. Nếu diện tích và một trong hai kích thước đã biết, bạn có thể tìm kích thước còn lại bằng cách:
\[
l = \frac{A}{w}
\]
hoặc
\[
w = \frac{A}{l}
\]
Ví dụ:
- Giả sử diện tích của mảnh vải là 120 cm2 và chiều rộng là 10 cm. Để tìm chiều dài, bạn sử dụng công thức:
\[
l = \frac{120}{10} = 12 \text{ cm}
\]
Bằng cách áp dụng các bước trên, bạn có thể tìm kích thước của mảnh vải một cách chính xác.
Bài Tập 10: Tính Số Lượng Mẫu Trong Dữ Liệu
Để tính số lượng mẫu trong một tập dữ liệu, bạn cần xác định số lượng các giá trị khác nhau hoặc số lượng các mẫu được lấy từ tập dữ liệu. Dưới đây là hướng dẫn chi tiết để thực hiện điều này:
Bước 1: Xác định tập dữ liệu cần phân tích. Tập dữ liệu có thể là một danh sách các giá trị hoặc số liệu được thu thập từ một nguồn cụ thể.
Bước 2: Xác định số lượng mẫu trong tập dữ liệu. Số lượng mẫu thường được biểu thị bằng số lượng các giá trị trong tập dữ liệu.
Bước 3: Nếu bạn muốn tính số lượng các mẫu khác nhau (hay còn gọi là số lượng giá trị độc nhất), hãy đếm số lượng giá trị khác nhau trong tập dữ liệu.
Bước 4: Sử dụng công thức đơn giản để tính số lượng mẫu:
\[
n = \text{Số lượng mẫu}
\]
Trong đó:
- n là số lượng mẫu.
Bước 5: Nếu dữ liệu được phân loại theo nhóm, bạn có thể sử dụng bảng phân tích để đếm số lượng mẫu trong từng nhóm.
| Nhóm | Số lượng mẫu |
|---|---|
| Nhóm A | 15 |
| Nhóm B | 20 |
| Nhóm C | 10 |
Ví dụ:
- Giả sử bạn có tập dữ liệu sau: [5, 7, 8, 5, 9, 7, 10].
- Số lượng mẫu trong tập dữ liệu này là:
- Nếu bạn muốn tính số lượng giá trị độc nhất, bạn sẽ có: [5, 7, 8, 9, 10], tức là 5 giá trị độc nhất.
\[
n = 7
\]
Bằng cách áp dụng các bước trên, bạn có thể dễ dàng tính số lượng mẫu trong bất kỳ tập dữ liệu nào.

/https://cms-prod.s3-sgn09.fptcloud.com/Dua_an_mat_hay_nong_An_nhieu_dua_co_tot_khong_1_d2fe1469b0.jpeg)