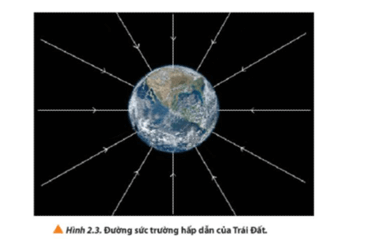
Chủ đề trường hấp dẫn chuyên đề lý 11: Chuyên đề "Trường hấp dẫn" trong môn Vật lý lớp 11 không chỉ giúp học sinh hiểu rõ nguyên lý hấp dẫn giữa các vật thể mà còn ứng dụng rộng rãi trong cuộc sống và nghiên cứu khoa học. Bài viết này sẽ dẫn dắt bạn qua các khái niệm cơ bản, phương pháp tính toán và ví dụ thực tiễn của trường hấp dẫn, từ đó khơi gợi niềm đam mê khám phá khoa học và xây dựng nền tảng vững chắc trong học tập.
Mục lục
Giới thiệu về trường hấp dẫn
Trường hấp dẫn là một khái niệm quan trọng trong vật lý, mô tả sự tác động qua lại giữa các vật có khối lượng trong không gian. Mỗi vật có khối lượng đều tạo ra một trường hấp dẫn xung quanh mình, và các vật thể khác đặt trong trường này sẽ chịu tác dụng của một lực gọi là lực hấp dẫn.
Khái niệm cơ bản: Trường hấp dẫn do một vật có khối lượng tạo ra là một loại trường lực, lan truyền từ vật đó ra xung quanh, ảnh hưởng đến các vật thể khác. Lực hấp dẫn giữa hai vật, ký hiệu là \( F \), được tính theo công thức:
\[
F = G \frac{m_1 m_2}{r^2}
\]
trong đó \( G \) là hằng số hấp dẫn, \( m_1 \) và \( m_2 \) là khối lượng của hai vật, và \( r \) là khoảng cách giữa chúng.
Vai trò của trường hấp dẫn:
- Trường hấp dẫn đóng vai trò quyết định trong việc duy trì các hành tinh trong hệ Mặt Trời chuyển động theo quỹ đạo của chúng.
- Trên Trái Đất, lực hấp dẫn là nguyên nhân khiến mọi vật rơi về phía mặt đất và tác động mạnh đến hoạt động của con người, đặc biệt là trong các lĩnh vực như hàng không và thiên văn học.
- Trong vũ trụ, lực hấp dẫn tạo nên sự liên kết giữa các thiên thể, hình thành nên các hệ sao, thiên hà, và nhiều cấu trúc lớn khác.
Trường hấp dẫn không chỉ là một khái niệm lý thuyết, mà còn có nhiều ứng dụng thực tế trong đời sống và nghiên cứu khoa học. Sự hiểu biết về trường hấp dẫn giúp chúng ta giải thích nhiều hiện tượng tự nhiên và phát triển các công nghệ ứng dụng trong khám phá không gian.

Phương pháp tính toán lực hấp dẫn
Trong vật lý, lực hấp dẫn là lực hút giữa hai vật có khối lượng, và để tính toán lực hấp dẫn giữa hai vật, ta sử dụng công thức Newton. Phương pháp này dựa trên các nguyên tắc về khối lượng của vật thể và khoảng cách giữa chúng trong không gian. Dưới đây là hướng dẫn chi tiết về phương pháp tính toán lực hấp dẫn:
-
Xác định khối lượng các vật: Đầu tiên, cần biết khối lượng của hai vật thể (ký hiệu là \( M \) và \( m \)). Khối lượng của vật càng lớn thì lực hấp dẫn giữa chúng càng lớn.
-
Xác định khoảng cách giữa hai vật: Khoảng cách giữa tâm hai vật thể (ký hiệu là \( r \)) là yếu tố quan trọng, bởi lực hấp dẫn tỷ lệ nghịch với bình phương khoảng cách này.
-
Sử dụng hằng số hấp dẫn: Hằng số hấp dẫn (ký hiệu \( G \)) là một giá trị cố định, thường là \( G = 6.674 \times 10^{-11} \, \text{N} \cdot \text{m}^2/\text{kg}^2 \).
-
Áp dụng công thức tính lực hấp dẫn: Công thức để tính lực hấp dẫn giữa hai vật thể là:
\( F = G \cdot \frac{M \cdot m}{r^2} \)
Trong đó:
- \( F \): Lực hấp dẫn (đơn vị Newton, N)
- \( M \) và \( m \): Khối lượng của hai vật (đơn vị kg)
- \( r \): Khoảng cách giữa hai vật (đơn vị m)
- \( G \): Hằng số hấp dẫn.
-
Tính toán cụ thể: Sau khi thay giá trị \( M \), \( m \), \( r \), và \( G \) vào công thức, ta có thể tính được lực hấp dẫn giữa hai vật. Ví dụ, lực hấp dẫn tác dụng lên một vật ở gần mặt đất có thể được tính toán dựa trên khối lượng Trái Đất và khoảng cách từ vật đến tâm Trái Đất.
Phương pháp trên là cơ bản cho việc tính toán lực hấp dẫn trong các bài toán về vật lý. Công thức này cũng giúp hiểu rõ hơn về các hiện tượng tự nhiên như chuyển động của hành tinh, lực hút của Trái Đất đối với các vật thể xung quanh, và các hiện tượng như thủy triều.
Ứng dụng của trường hấp dẫn trong đời sống và thiên văn học
Trường hấp dẫn có nhiều ứng dụng thiết thực không chỉ trong đời sống hằng ngày mà còn trong các nghiên cứu thiên văn học. Dưới đây là một số ứng dụng nổi bật:
- Trong đời sống:
- Ngành hàng không: Lực hấp dẫn giúp máy bay định hướng bay, tính toán quỹ đạo và kiểm soát cân bằng khi cất cánh và hạ cánh.
- Nghiên cứu khí hậu: Các mô hình khí hậu dựa trên lực hấp dẫn cho phép dự đoán và phân tích các hiện tượng thời tiết phức tạp như bão, lốc xoáy.
- Đo đạc và địa lý: Lực hấp dẫn còn được ứng dụng trong đo đạc địa hình, khảo sát độ cao và mật độ vật liệu dưới lòng đất phục vụ ngành địa chất.
- Trong thiên văn học:
- Chuyển động hành tinh: Lực hấp dẫn giữ các hành tinh trong quỹ đạo quanh Mặt Trời, giúp duy trì sự ổn định của Hệ Mặt Trời.
- Khám phá không gian: Các tàu vũ trụ sử dụng lực hấp dẫn của hành tinh để tiết kiệm nhiên liệu khi bay qua các hành tinh và khám phá vũ trụ.
- Quan sát thiên thể: Lực hấp dẫn giúp các nhà khoa học hiểu rõ hơn về sự hình thành và phát triển của các thiên hà, sao và hành tinh mới.
Các ứng dụng trên cho thấy tầm quan trọng của lực hấp dẫn, không chỉ hỗ trợ các hoạt động trên Trái Đất mà còn mở rộng hiểu biết về vũ trụ và cách nó hoạt động.
Các hiện tượng liên quan đến trường hấp dẫn
Trường hấp dẫn có vai trò quan trọng trong nhiều hiện tượng tự nhiên và hiện tượng thiên văn. Dưới đây là một số hiện tượng tiêu biểu có liên quan đến trường hấp dẫn:
- Hiện tượng rơi tự do
Một vật được thả từ độ cao sẽ chịu tác động của lực hấp dẫn từ Trái Đất, làm cho nó rơi xuống với gia tốc \(g \approx 9.8 \, m/s^2\). Hiện tượng này minh chứng cho lực hấp dẫn mà Trái Đất tác động lên các vật thể xung quanh.
- Chuyển động của các hành tinh
Hành tinh di chuyển theo quỹ đạo quanh Mặt Trời là do lực hấp dẫn của Mặt Trời. Lực này giữ cho các hành tinh không bị bay ra ngoài không gian mà duy trì quỹ đạo quay quanh Mặt Trời.
- Thủy triều
Thủy triều là kết quả của lực hấp dẫn giữa Trái Đất và Mặt Trăng. Lực hấp dẫn của Mặt Trăng kéo nước trên các đại dương, gây ra hiện tượng thủy triều lên xuống hàng ngày.
- Hiện tượng giãn nở thời gian gần hố đen
Gần các vật thể có khối lượng cực lớn như hố đen, thời gian giãn nở theo lý thuyết tương đối tổng quát của Einstein. Hiện tượng này làm cho thời gian trôi chậm lại so với vùng có trường hấp dẫn yếu hơn.
Các hiện tượng trên cho thấy tầm ảnh hưởng rộng lớn của trường hấp dẫn không chỉ trên Trái Đất mà còn trong các hệ thống thiên văn. Trường hấp dẫn giúp chúng ta hiểu rõ hơn về cách các hành tinh vận hành và ảnh hưởng của các lực tự nhiên.
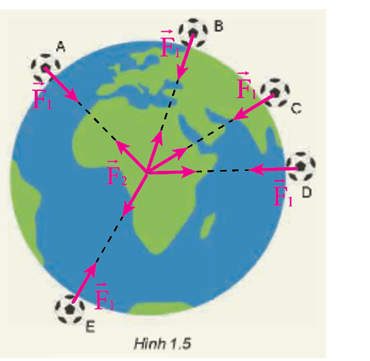
Phân tích chuyên sâu về các ví dụ điển hình
Các hiện tượng liên quan đến trường hấp dẫn được biểu diễn qua nhiều ví dụ thực tiễn, giúp chúng ta hiểu rõ hơn về vai trò của lực hấp dẫn trong vũ trụ và đời sống. Dưới đây là một số ví dụ điển hình thường được phân tích sâu trong chuyên đề trường hấp dẫn Lý 11:
1. Lực Hấp Dẫn giữa Trái Đất và Vật Thể Rơi
- Trái Đất tác dụng một lực hấp dẫn lên mọi vật thể trong không gian của nó. Lực này thường được biểu diễn qua công thức: \[ F = G \dfrac{m_1 \cdot m_2}{r^2} \] trong đó \( F \) là lực hấp dẫn giữa hai vật, \( G \) là hằng số hấp dẫn, \( m_1 \) và \( m_2 \) là khối lượng của hai vật, và \( r \) là khoảng cách giữa chúng.
- Ví dụ: Lực hấp dẫn tác dụng lên quả táo khi nó rơi tự do về phía Trái Đất. Do khối lượng Trái Đất rất lớn, chúng ta không cảm nhận được sự chuyển động của nó về phía quả táo, mà chỉ thấy quả táo rơi xuống.
2. Trường Hấp Dẫn Giữa Các Hành Tinh trong Hệ Mặt Trời
Trong hệ Mặt Trời, lực hấp dẫn của Mặt Trời đóng vai trò giữ các hành tinh chuyển động quay quanh nó, tạo thành quỹ đạo ổn định. Ví dụ:
- Quỹ đạo của Trái Đất xung quanh Mặt Trời là kết quả của lực hấp dẫn từ Mặt Trời tác dụng lên Trái Đất.
- Các hành tinh lớn hơn, như Sao Mộc và Sao Thổ, cũng tạo ra trường hấp dẫn mạnh, ảnh hưởng tới các vật thể gần chúng.
3. Hiện Tượng Sóng Hấp Dẫn
- Sóng hấp dẫn được phát hiện khi hai vật thể có khối lượng lớn, như hai lỗ đen, quay quanh nhau và dần hợp nhất. Sự thay đổi trong trường hấp dẫn tạo ra sóng hấp dẫn lan truyền trong không gian.
- Ví dụ điển hình là sự hợp nhất của hai lỗ đen cách đây hàng triệu năm, nhưng sóng hấp dẫn của chúng mới chỉ đến Trái Đất gần đây và đã được các nhà khoa học phát hiện.
4. Hiện Tượng Mặt Trăng Ảnh Hưởng Thủy Triều
Lực hấp dẫn giữa Trái Đất và Mặt Trăng là nguyên nhân chính gây ra hiện tượng thủy triều. Các giai đoạn của thủy triều cao và thấp thay đổi theo vị trí của Mặt Trăng và Trái Đất, với:
| Hiện Tượng | Mô Tả |
|---|---|
| Thủy triều cao | Xảy ra khi Mặt Trăng nằm thẳng hàng với một điểm trên Trái Đất, lực hấp dẫn từ Mặt Trăng kéo nước biển dâng lên. |
| Thủy triều thấp | Xảy ra khi Mặt Trăng không thẳng hàng với điểm đó, nước biển sẽ rút xuống dưới tác động của trọng lực Trái Đất. |
Kết luận
Các ví dụ điển hình trên đây cho thấy trường hấp dẫn không chỉ ảnh hưởng đến các vật thể gần chúng mà còn là nguyên nhân của nhiều hiện tượng trong vũ trụ. Qua các bài học và ví dụ thực tiễn, học sinh có thể hiểu rõ hơn về tính chất và vai trò của lực hấp dẫn trong các hiện tượng vật lý.
Thực hành và câu hỏi thường gặp
Trong phần này, chúng ta sẽ khám phá một số bài tập thực hành và trả lời các câu hỏi phổ biến về trường hấp dẫn, đặc biệt là những câu hỏi thường gặp trong các bài học Vật Lý lớp 11.
Bài tập thực hành
-
Bài tập 1: Tính lực hấp dẫn giữa hai quả cầu
Hai quả cầu, mỗi quả có khối lượng 5 kg và khoảng cách giữa tâm của chúng là 1 m. Tính lực hấp dẫn giữa chúng.
Giải: Áp dụng công thức lực hấp dẫn:
\[
F = G \frac{m_1 m_2}{r^2}
\]Thay giá trị vào: \( G = 6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2 \), \( m_1 = 5 \, \text{kg} \), \( m_2 = 5 \, \text{kg} \), \( r = 1 \, \text{m} \), ta có:
\[
F = 6.674 \times 10^{-11} \frac{5 \times 5}{1^2} = 1.6685 \times 10^{-9} \, \text{N}
\]Lực hấp dẫn giữa hai quả cầu là \(1.6685 \times 10^{-9}\) N.
-
Bài tập 2: So sánh lực hấp dẫn và trọng lực
Với một vật có khối lượng 1 kg đặt trên bề mặt Trái Đất, tính trọng lực tác dụng lên vật và so sánh với lực hấp dẫn của vật với một quả bóng có khối lượng 2 kg, cách vật 1 m.
Giải:
- Trọng lực: \( P = mg \)
- Với \( m = 1 \, \text{kg} \) và \( g = 9.8 \, \text{m/s}^2 \), ta có \( P = 1 \times 9.8 = 9.8 \, \text{N} \).
- Lực hấp dẫn giữa hai vật: \[ F = G \frac{m_1 m_2}{r^2} \]
- Với \( m_1 = 1 \, \text{kg} \), \( m_2 = 2 \, \text{kg} \), \( r = 1 \, \text{m} \), ta có:
- \[ F = 6.674 \times 10^{-11} \frac{1 \times 2}{1^2} = 1.3348 \times 10^{-10} \, \text{N} \]
So với trọng lực 9.8 N, lực hấp dẫn giữa hai vật nhỏ hơn rất nhiều.
Câu hỏi thường gặp
-
Hỏi: Tại sao lực hấp dẫn của Trái Đất tác dụng lên các vật lại mạnh mẽ như vậy?
Đáp: Vì Trái Đất có khối lượng rất lớn nên trường hấp dẫn của nó đủ mạnh để giữ mọi vật trên bề mặt, tạo ra cảm giác trọng lực mà chúng ta cảm nhận được.
-
Hỏi: Trường hấp dẫn có tồn tại trong chân không không?
Đáp: Có, trường hấp dẫn không phụ thuộc vào môi trường, và nó tồn tại cả trong chân không. Điều này có nghĩa là các vật có khối lượng sẽ luôn hấp dẫn lẫn nhau bất kể không gian xung quanh.
-
Hỏi: Cường độ trường hấp dẫn là gì và có đơn vị đo nào?
Đáp: Cường độ trường hấp dẫn tại một điểm là lực hấp dẫn tác dụng lên một đơn vị khối lượng tại điểm đó, và có đơn vị là N/kg.
Qua các bài tập và câu hỏi này, học sinh sẽ hiểu rõ hơn về cách áp dụng công thức trường hấp dẫn và bản chất của lực hấp dẫn trong các tình huống thực tế.