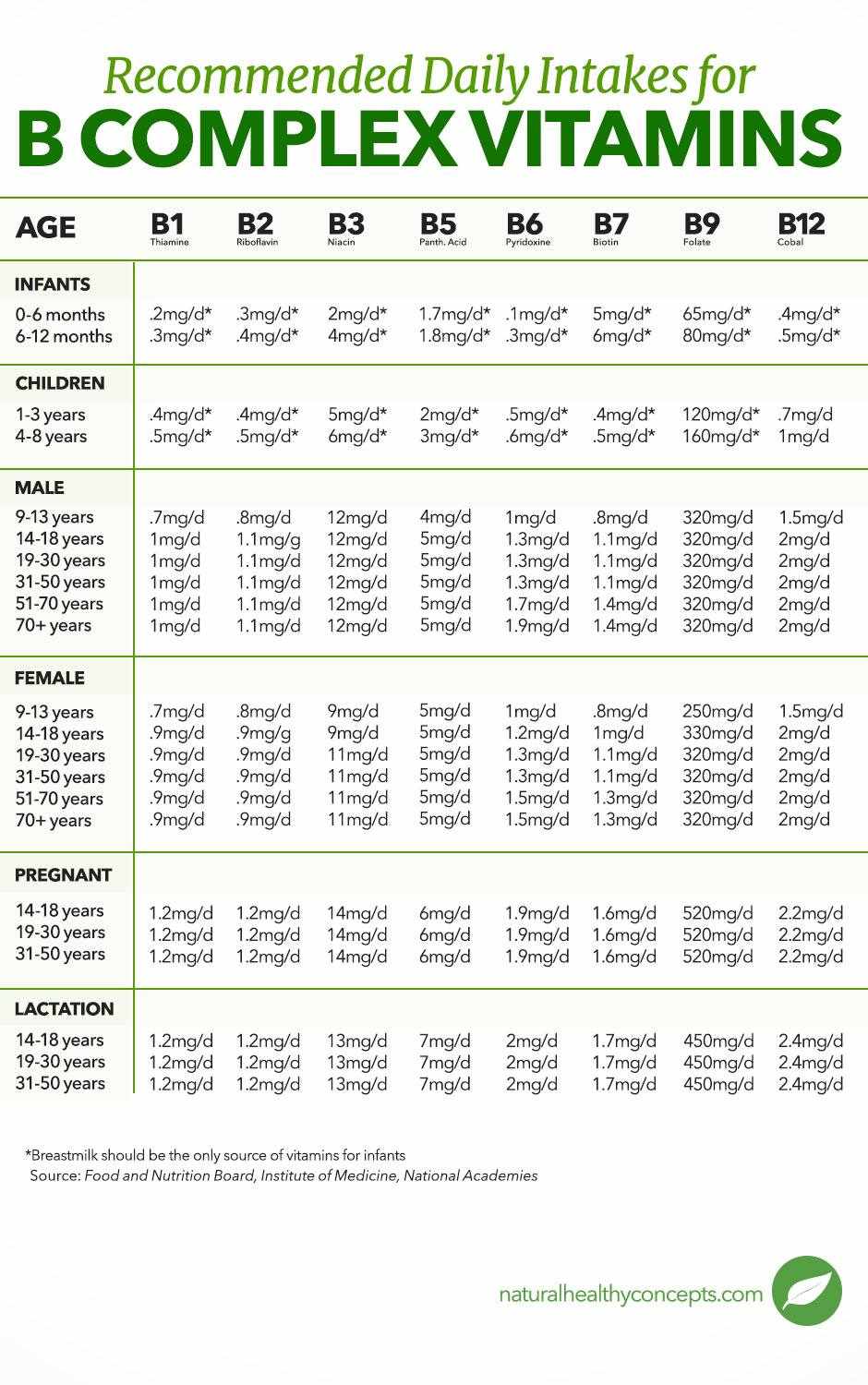
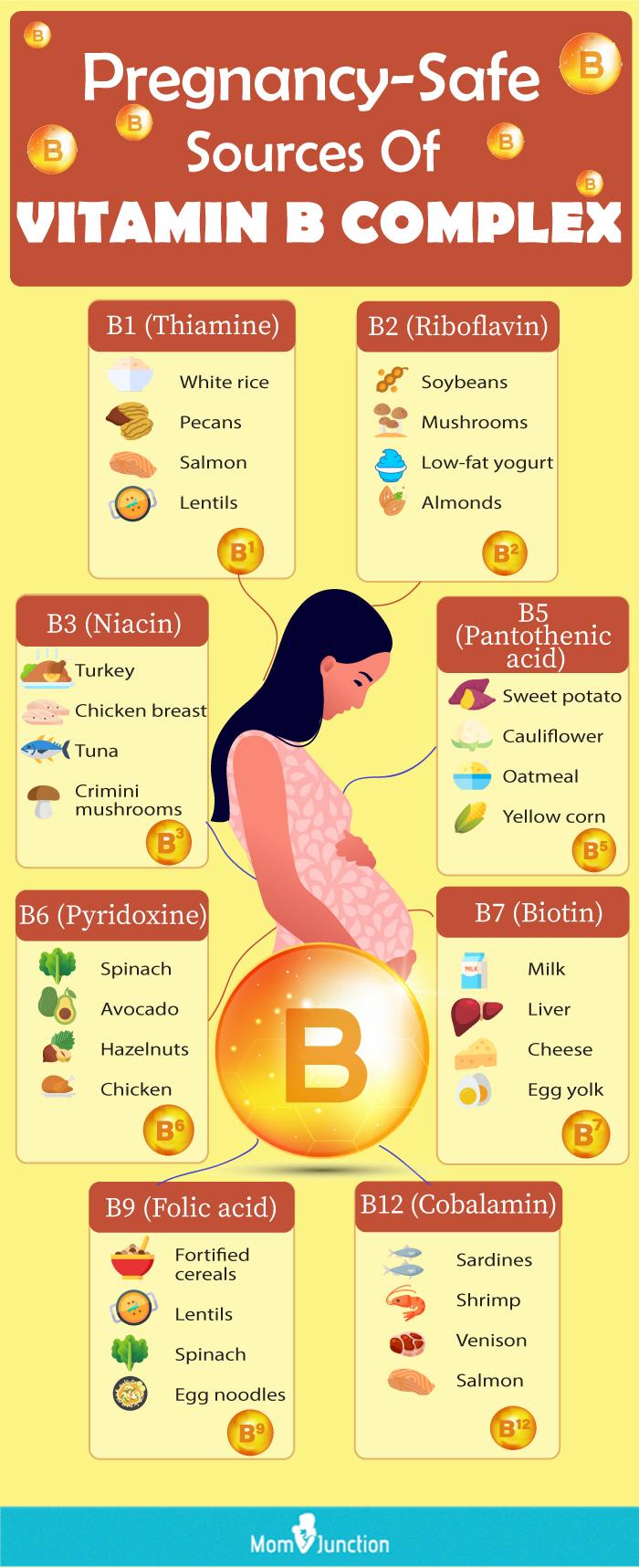
Chủ đề vitamin b complex with zinc capsules uses: Vitamin B Complex with Zinc Capsules là sự kết hợp hoàn hảo giữa các vitamin nhóm B và kẽm, giúp tăng cường hệ miễn dịch, cải thiện sức khỏe tinh thần và thể chất. Với công dụng hỗ trợ điều trị thiếu hụt dinh dưỡng, sản phẩm này mang lại lợi ích toàn diện cho người dùng, đặc biệt là những ai cần bổ sung vitamin và khoáng chất.
Mục lục
- Công dụng và lợi ích của Vitamin B Complex với kẽm
- Hướng dẫn sử dụng
- Hướng dẫn sử dụng
- Công dụng của Vitamin B Complex with Zinc Capsules
- Thành phần chính trong Vitamin B Complex with Zinc Capsules
- Liều dùng và cách sử dụng
- Tác dụng phụ có thể gặp
- Đối tượng sử dụng phù hợp
- Lưu ý khi sử dụng Vitamin B Complex with Zinc Capsules
- 10 Dạng Bài Tập Toán, Lý hoặc Tiếng Anh
- Dạng bài tập 1: Giải phương trình bậc hai trong Toán học
- Dạng bài tập 2: Tìm giao điểm của hai đường thẳng
- Dạng bài tập 3: Xác định tam giác đồng dạng
- Dạng bài tập 4: Tính toán sức cản không khí trong Vật lý
- Dạng bài tập 5: Dịch câu điều kiện loại 3 trong Tiếng Anh
- Dạng bài tập 6: Tìm ma trận nghịch đảo trong Đại số
- Dạng bài tập 7: Giải hệ phương trình bậc nhất hai ẩn
- Dạng bài tập 8: Tính vận tốc trung bình trong chuyển động thẳng
- Dạng bài tập 9: Hoàn thành đoạn hội thoại trong Tiếng Anh
- Dạng bài tập 10: Tính diện tích hình tròn trong Toán học
Công dụng và lợi ích của Vitamin B Complex với kẽm
Vitamin B Complex kết hợp với kẽm là một sản phẩm bổ sung được sử dụng rộng rãi để hỗ trợ sức khỏe tổng thể, cung cấp năng lượng và duy trì các chức năng quan trọng của cơ thể. Sau đây là một số công dụng nổi bật:
1. Tăng cường sức khỏe hệ miễn dịch
Vitamin B Complex và kẽm giúp củng cố hệ miễn dịch, bảo vệ cơ thể khỏi các bệnh tật thông qua việc sản sinh năng lượng và hỗ trợ quá trình chuyển hóa dưỡng chất.
- Các vitamin B1, B2, B6 và B12 hỗ trợ quá trình chuyển hóa carbohydrate, protein và chất béo, cung cấp năng lượng cho cơ thể.
- Kẽm đóng vai trò quan trọng trong việc duy trì sức khỏe của tế bào miễn dịch.
2. Cải thiện sức khỏe da, tóc và móng
Việc sử dụng vitamin B Complex kết hợp với kẽm còn có tác dụng tốt đối với sức khỏe da, tóc và móng. Đặc biệt, vitamin B7 (biotin) và kẽm hỗ trợ cấu trúc và sự phát triển của tóc và móng.
- Biotin (B7) được biết đến với vai trò cải thiện sức khỏe của tóc, móng và da.
- Kẽm giúp tăng cường khả năng tái tạo tế bào và hỗ trợ sức khỏe da.
3. Hỗ trợ sức khỏe thần kinh và tâm lý
Vitamin B Complex cũng có tác dụng hỗ trợ hệ thần kinh, giúp giảm căng thẳng, lo âu và cải thiện tinh thần. Kẽm đóng vai trò quan trọng trong việc duy trì chức năng não bộ và cân bằng cảm xúc.
- Vitamin B6 và B12 có tác dụng hỗ trợ sản xuất chất dẫn truyền thần kinh, giúp giảm căng thẳng và cải thiện tâm lý.
- Kẽm giúp cải thiện trí nhớ và sự tập trung.
4. Phòng ngừa các bệnh lý tim mạch
Bổ sung vitamin B Complex với kẽm giúp giảm nguy cơ mắc các bệnh về tim mạch. Vitamin B12 đặc biệt có vai trò trong việc duy trì nồng độ homocysteine, một chỉ số quan trọng liên quan đến sức khỏe tim mạch.
- Vitamin B12 và B6 hỗ trợ giảm mức homocysteine, giúp phòng ngừa các bệnh về tim.
- Kẽm góp phần cải thiện tuần hoàn máu và sức khỏe mạch máu.
5. Hỗ trợ quá trình sản xuất năng lượng
Các vitamin nhóm B tham gia vào quá trình chuyển hóa năng lượng trong cơ thể, từ đó giúp duy trì sức sống và năng lượng hàng ngày. Kẽm cũng đóng vai trò quan trọng trong quá trình này.
- Vitamin B1 (thiamine) giúp biến đổi carbohydrate thành năng lượng.
- Kẽm giúp tăng hiệu suất của quá trình trao đổi chất.
6. Cải thiện sức khỏe tiêu hóa
Bổ sung vitamin B Complex với kẽm giúp tăng cường hoạt động tiêu hóa và hỗ trợ quá trình hấp thụ dưỡng chất.
- Vitamin B2 và B3 giúp cải thiện chức năng tiêu hóa.
- Kẽm hỗ trợ sự phân hủy và hấp thụ dưỡng chất.
Hướng dẫn sử dụng
Thông thường, viên uống vitamin B Complex với kẽm được khuyến cáo sử dụng 1 viên mỗi ngày sau bữa ăn hoặc theo chỉ định của bác sĩ.
Với việc bổ sung đầy đủ vitamin B Complex và kẽm, người dùng sẽ nhận được nhiều lợi ích cho sức khỏe tổng thể, bao gồm tăng cường năng lượng, hỗ trợ hệ miễn dịch và cải thiện sức khỏe da, tóc, móng.
Hướng dẫn sử dụng
Thông thường, viên uống vitamin B Complex với kẽm được khuyến cáo sử dụng 1 viên mỗi ngày sau bữa ăn hoặc theo chỉ định của bác sĩ.
Với việc bổ sung đầy đủ vitamin B Complex và kẽm, người dùng sẽ nhận được nhiều lợi ích cho sức khỏe tổng thể, bao gồm tăng cường năng lượng, hỗ trợ hệ miễn dịch và cải thiện sức khỏe da, tóc, móng.
Công dụng của Vitamin B Complex with Zinc Capsules
Vitamin B Complex với kẽm mang lại nhiều lợi ích cho sức khỏe, đặc biệt là:
- Hỗ trợ sức khỏe thần kinh: Vitamin B1, B6 và B12 đóng vai trò quan trọng trong việc bảo vệ các tế bào thần kinh và cải thiện chức năng của hệ thần kinh.
- Tăng cường hệ miễn dịch: Kẽm giúp cải thiện sức đề kháng, bảo vệ cơ thể chống lại vi khuẩn và virus gây bệnh.
- Thúc đẩy quá trình trao đổi chất: Vitamin B đóng vai trò then chốt trong việc chuyển hóa chất dinh dưỡng thành năng lượng, giúp cơ thể duy trì năng lượng cả ngày.
- Hỗ trợ sản xuất hồng cầu: Vitamin B12 và B6 giúp sản sinh hồng cầu, ngăn ngừa thiếu máu và cung cấp đủ oxy cho các mô.
- Giảm căng thẳng và mệt mỏi: Vitamin B và kẽm giúp giảm thiểu căng thẳng, mệt mỏi và duy trì sức khỏe tinh thần ổn định.
Công thức kết hợp giữa các vitamin nhóm B và kẽm mang lại tác động toàn diện, hỗ trợ sức khỏe thể chất và tinh thần, đồng thời tăng cường khả năng hấp thụ dưỡng chất.
Thành phần chính trong Vitamin B Complex with Zinc Capsules
Vitamin B Complex with Zinc Capsules chứa sự kết hợp của các thành phần dinh dưỡng quan trọng giúp tăng cường sức khỏe toàn diện:
- Vitamin B1 (Thiamine): Hỗ trợ quá trình chuyển hóa carbohydrate và tăng cường sức khỏe thần kinh.
- Vitamin B2 (Riboflavin): Cần thiết cho sản xuất năng lượng và duy trì chức năng của các tế bào cơ thể.
- Vitamin B3 (Niacin): Giúp cải thiện tuần hoàn máu và hỗ trợ hệ tiêu hóa khỏe mạnh.
- Vitamin B6 (Pyridoxine): Quan trọng trong việc tổng hợp hemoglobin và duy trì chức năng não bộ.
- Vitamin B12 (Cyanocobalamin): Cần thiết cho quá trình sản xuất hồng cầu và duy trì hệ thần kinh khỏe mạnh.
- Vitamin B5 (Pantothenic Acid): Tham gia vào quá trình tổng hợp coenzyme A, quan trọng cho sự trao đổi chất.
- Vitamin B7 (Biotin): Hỗ trợ sức khỏe làn da, tóc và móng.
- Kẽm (Zinc): Một khoáng chất thiết yếu giúp tăng cường hệ miễn dịch, chữa lành vết thương và thúc đẩy chức năng enzym trong cơ thể.
Sự kết hợp giữa các vitamin nhóm B và kẽm giúp duy trì sức khỏe toàn diện, cung cấp dưỡng chất thiết yếu cho cơ thể, đặc biệt là trong việc tăng cường năng lượng và bảo vệ hệ miễn dịch.
Liều dùng và cách sử dụng
Để đạt hiệu quả tối ưu từ Vitamin B Complex with Zinc Capsules, cần tuân thủ liều dùng và cách sử dụng sau:
- Liều dùng: Mỗi ngày uống 1-2 viên, tùy thuộc vào nhu cầu dinh dưỡng và sự chỉ định của bác sĩ.
- Cách sử dụng: Uống viên nang với nước sau bữa ăn, tốt nhất là vào buổi sáng để cơ thể hấp thụ dưỡng chất tốt nhất.
- Lưu ý: Không nên dùng quá liều quy định và tránh sử dụng cho người dị ứng với bất kỳ thành phần nào trong sản phẩm.
- Trẻ em và phụ nữ mang thai: Cần tham khảo ý kiến bác sĩ trước khi sử dụng.
Việc tuân thủ liều lượng và cách sử dụng đúng cách sẽ giúp tăng cường hiệu quả của sản phẩm, đảm bảo an toàn và sức khỏe cho người sử dụng.
Tác dụng phụ có thể gặp
Vitamin B Complex with Zinc Capsules nhìn chung là an toàn khi sử dụng đúng liều lượng, nhưng một số tác dụng phụ hiếm gặp có thể bao gồm:
- Rối loạn tiêu hóa: Có thể gặp phải tình trạng buồn nôn, đầy hơi hoặc tiêu chảy nhẹ khi dùng quá liều hoặc đối với người nhạy cảm với các thành phần trong sản phẩm.
- Dị ứng da: Một số người có thể bị nổi mẩn, ngứa, hoặc sưng tại các vùng da sau khi sử dụng viên nang.
- Chóng mặt hoặc đau đầu: Có thể xảy ra khi cơ thể phản ứng với liều lượng cao vitamin hoặc kẽm.
- Mất ngủ: Dùng viên nang vào buổi tối có thể gây khó ngủ đối với những người nhạy cảm với vitamin nhóm B.
Nếu gặp bất kỳ tác dụng phụ nào, nên ngừng sử dụng và tham khảo ý kiến bác sĩ để được hướng dẫn cụ thể.
Đối tượng sử dụng phù hợp
Vitamin B Complex with Zinc Capsules là sản phẩm bổ sung dinh dưỡng được thiết kế để đáp ứng nhu cầu của nhiều đối tượng khác nhau:
- Người bị thiếu hụt vitamin B và kẽm: Sản phẩm phù hợp cho những người có chế độ ăn uống thiếu vitamin B và kẽm, thường gặp ở người ăn chay hoặc ăn uống không cân đối.
- Người mệt mỏi, căng thẳng: Vitamin B giúp tăng cường năng lượng, hỗ trợ hệ thần kinh, rất hữu ích cho những người thường xuyên căng thẳng hoặc làm việc quá sức.
- Người có vấn đề về da, tóc, móng: Kẽm và các vitamin B có vai trò quan trọng trong việc duy trì sức khỏe của da, tóc và móng, giúp ngăn ngừa rụng tóc, khô da.
- Phụ nữ mang thai và cho con bú: Sản phẩm có thể được khuyến nghị cho phụ nữ mang thai hoặc đang cho con bú, nhưng cần tham khảo ý kiến bác sĩ trước khi sử dụng.
- Người có hệ miễn dịch yếu: Kẽm và vitamin B hỗ trợ hệ miễn dịch, giúp cơ thể chống lại bệnh tật và hồi phục nhanh hơn.
Sản phẩm không phù hợp cho trẻ nhỏ dưới 12 tuổi, người dị ứng với bất kỳ thành phần nào trong viên nang, hoặc người đang dùng thuốc có chứa hàm lượng kẽm cao.
Lưu ý khi sử dụng Vitamin B Complex with Zinc Capsules
Trong quá trình sử dụng Vitamin B Complex with Zinc Capsules, người dùng cần lưu ý một số điểm quan trọng để đảm bảo an toàn và hiệu quả:
- Tham khảo ý kiến bác sĩ: Trước khi bắt đầu sử dụng, đặc biệt nếu bạn đang mang thai, cho con bú, hoặc đang dùng các loại thuốc khác, hãy tham khảo ý kiến của bác sĩ để tránh tác dụng phụ hoặc tương tác thuốc không mong muốn.
- Liều dùng hợp lý: Không nên tự ý tăng liều dùng mà cần tuân thủ đúng liều lượng được chỉ định trên bao bì hoặc theo chỉ dẫn của chuyên gia y tế. Sử dụng quá liều có thể gây ra những tác dụng phụ nghiêm trọng.
- Tránh dùng cùng các sản phẩm bổ sung khác: Nếu bạn đang sử dụng các sản phẩm có chứa kẽm hoặc vitamin B khác, hãy thận trọng để tránh việc dư thừa các dưỡng chất, gây hại cho sức khỏe.
- Lưu trữ đúng cách: Bảo quản sản phẩm ở nơi khô ráo, thoáng mát, tránh ánh nắng trực tiếp và xa tầm tay trẻ em.
- Ngưng sử dụng khi có dấu hiệu dị ứng: Nếu bạn gặp bất kỳ dấu hiệu dị ứng nào như phát ban, ngứa, hoặc sưng, hãy ngừng sử dụng ngay lập tức và liên hệ với bác sĩ.
Bằng cách tuân thủ các lưu ý trên, bạn có thể sử dụng sản phẩm một cách an toàn và đạt được hiệu quả tốt nhất cho sức khỏe của mình.
10 Dạng Bài Tập Toán, Lý hoặc Tiếng Anh
Dưới đây là 10 dạng bài tập Toán, Lý và Tiếng Anh phổ biến dành cho học sinh, giúp các em nắm vững kiến thức và nâng cao kỹ năng thực hành:
- Toán học:
- Dạng 1: Giải phương trình bậc 2 \[ ax^2 + bx + c = 0 \]
- Dạng 2: Hình học không gian - Tính thể tích và diện tích
- Dạng 3: Xác suất và thống kê - Tìm xác suất của một biến cố
- Dạng 4: Bài toán tối ưu hóa - Tìm giá trị lớn nhất, nhỏ nhất
- Dạng 5: Hệ phương trình tuyến tính \[ \begin{cases} ax + by = c \\ dx + ey = f \end{cases} \]
- Vật lý:
- Dạng 1: Chuyển động thẳng đều - Tính vận tốc, quãng đường, thời gian
- Dạng 2: Định luật bảo toàn năng lượng - Tính công và năng lượng của một hệ
- Dạng 3: Hiện tượng sóng cơ - Tính tần số và bước sóng
- Dạng 4: Mạch điện xoay chiều - Tính tổng trở, cường độ dòng điện
- Dạng 5: Hiện tượng quang điện - Tính năng lượng photon
- Tiếng Anh:
- Dạng 1: Viết lại câu giữ nguyên nghĩa
- Dạng 2: Điền từ vào đoạn văn
- Dạng 3: Chia động từ theo thì
- Dạng 4: Viết luận theo chủ đề
- Dạng 5: Bài tập đọc hiểu và trả lời câu hỏi
Các dạng bài tập trên sẽ giúp học sinh luyện tập toàn diện cả về lý thuyết lẫn thực hành, giúp nâng cao kỹ năng và thành tích học tập.

Dạng bài tập 1: Giải phương trình bậc hai trong Toán học
Phương trình bậc hai có dạng tổng quát như sau:
Trong đó:
- \(a\), \(b\), \(c\) là các hằng số (với \(a \neq 0\))
- \(x\) là ẩn số cần tìm
Để giải phương trình bậc hai, ta áp dụng công thức nghiệm sau:
Quá trình giải phương trình bậc hai được thực hiện theo các bước:
- Xác định các hệ số: Đầu tiên, xác định giá trị của \(a\), \(b\), \(c\) từ phương trình.
- Tính biệt thức (delta): Sử dụng công thức:
\[
\Delta = b^2 - 4ac
\]
- Nếu \(\Delta > 0\): Phương trình có hai nghiệm phân biệt.
- Nếu \(\Delta = 0\): Phương trình có nghiệm kép.
- Nếu \(\Delta < 0\): Phương trình vô nghiệm trong tập số thực.
- Tìm nghiệm: Áp dụng công thức nghiệm để tìm \(x_1\) và \(x_2\) (nếu có).
Ví dụ: Giải phương trình sau:
Ta có:
- \(a = 2\)
- \(b = -4\)
- \(c = 2\)
Tính biệt thức:
Vì \(\Delta = 0\), phương trình có nghiệm kép:
Vậy nghiệm của phương trình là \(x = 1\).
Dạng bài tập 2: Tìm giao điểm của hai đường thẳng
Để tìm giao điểm của hai đường thẳng, chúng ta cần giải hệ phương trình biểu diễn các đường thẳng đó.
Giả sử hai đường thẳng được cho bởi phương trình:
- \( y = m_1x + b_1 \)
- \( y = m_2x + b_2 \)
Bước 1: Đặt phương trình hai đường thẳng bằng nhau:
Bước 2: Chuyển đổi phương trình để tìm \( x \):
Bước 3: Thay giá trị \( x \) vào một trong hai phương trình để tìm \( y \):
Vậy, giao điểm của hai đường thẳng là tọa độ \( (x, y) \).
Ví dụ: Cho hai đường thẳng:
- \( y = 2x + 3 \)
- \( y = -x + 1 \)
Giải hệ phương trình:
Thay \( x = -\frac{2}{3} \) vào phương trình thứ nhất:
Vậy giao điểm của hai đường thẳng là \( \left(-\frac{2}{3}, \frac{5}{3}\right) \).
Dạng bài tập 3: Xác định tam giác đồng dạng
Để xác định hai tam giác đồng dạng, chúng ta có thể áp dụng các tiêu chí đồng dạng như sau:
- Tiêu chí góc-góc (AA): Nếu hai góc của tam giác này bằng hai góc của tam giác kia, thì hai tam giác đó đồng dạng.
- Tiêu chí cạnh-góc-cạnh (SAS): Nếu tỉ lệ hai cạnh tương ứng của hai tam giác bằng nhau và góc xen giữa hai cạnh đó bằng nhau, thì hai tam giác đó đồng dạng.
- Tiêu chí cạnh-cạnh-cạnh (SSS): Nếu tỉ lệ ba cạnh tương ứng của hai tam giác bằng nhau, thì hai tam giác đó đồng dạng.
Ví dụ: Cho tam giác \( ABC \) và tam giác \( DEF \), biết rằng:
- \( \angle A = \angle D \)
- \( \angle B = \angle E \)
Vì hai góc của tam giác \( ABC \) bằng hai góc của tam giác \( DEF \), theo tiêu chí góc-góc (AA), ta kết luận rằng:
Ví dụ 2: Cho tam giác \( GHI \) và tam giác \( JKL \), biết rằng:
- \( \frac{GH}{JK} = \frac{HI}{KL} \)
- \( \angle H = \angle K \)
Theo tiêu chí cạnh-góc-cạnh (SAS), ta kết luận rằng:
Vậy, hai tam giác này đồng dạng theo tiêu chí SAS.

Dạng bài tập 4: Tính toán sức cản không khí trong Vật lý
Sức cản không khí là lực cản xuất hiện khi một vật di chuyển trong môi trường không khí. Lực này có thể được tính bằng công thức:
Trong đó:
- \( F \) là lực cản không khí (N).
- \( C_d \) là hệ số cản của vật (không có đơn vị).
- \( A \) là diện tích cản của vật theo phương ngang (m²).
- \( \rho \) là mật độ không khí (kg/m³).
- \( v \) là vận tốc của vật (m/s).
Ví dụ: Một chiếc xe có diện tích cản \( A = 2.5 \, m^2 \), hệ số cản \( C_d = 0.3 \), vận tốc di chuyển \( v = 30 \, m/s \), và mật độ không khí \( \rho = 1.2 \, kg/m^3 \). Tính lực cản không khí tác dụng lên xe.
Áp dụng công thức:
Ta tính được:
Vậy, lực cản không khí tác dụng lên xe là 405 Newton.
Dạng bài tập 5: Dịch câu điều kiện loại 3 trong Tiếng Anh
Câu điều kiện loại 3 được sử dụng để diễn tả những sự việc không có thật trong quá khứ và giả định về một kết quả khác nếu điều kiện thay đổi. Cấu trúc của câu điều kiện loại 3 như sau:
Ví dụ:
- Câu gốc: If she had studied harder, she would have passed the exam.
- Dịch: Nếu cô ấy học chăm chỉ hơn, cô ấy đã đỗ kỳ thi.
Phân tích:
- Phần "If she had studied harder" là điều kiện giả định không có thật trong quá khứ.
- Phần "she would have passed the exam" là kết quả mà sẽ xảy ra nếu điều kiện được thỏa mãn.
Bài tập dịch:
- If they had arrived earlier, they would have seen the performance.
- If he had known about the party, he would have attended.
Hãy thử dịch các câu trên và phân tích theo cấu trúc câu điều kiện loại 3.
Dạng bài tập 6: Tìm ma trận nghịch đảo trong Đại số
Ma trận nghịch đảo của một ma trận vuông \( A \) là ma trận \( A^{-1} \) sao cho:
Trong đó \( I \) là ma trận đơn vị. Để tìm ma trận nghịch đảo, ta làm theo các bước sau:
- Kiểm tra xem ma trận \( A \) có khả nghịch không bằng cách tính định thức \(\det(A)\). Nếu \(\det(A) = 0\), ma trận không khả nghịch và không có ma trận nghịch đảo.
- Tính ma trận phụ hợp (adjugate) của ma trận \( A \), tức là tìm ma trận các phần bù đại số của các phần tử của ma trận.
- Ma trận nghịch đảo \( A^{-1} \) được tính theo công thức: \[ A^{-1} = \frac{1}{\det(A)} \times \text{adj}(A) \]
Ví dụ:
Cho ma trận \( A \) như sau:
Bước 1: Tính định thức của \( A \):
Bước 2: Tìm ma trận phụ hợp (adjugate):
Bước 3: Tính ma trận nghịch đảo:
Vậy ma trận nghịch đảo của \( A \) là:
Dạng bài tập 7: Giải hệ phương trình bậc nhất hai ẩn
Hệ phương trình bậc nhất hai ẩn là hệ phương trình có dạng:
Để giải hệ phương trình này, ta có thể sử dụng các phương pháp sau:
- Phương pháp thế:
- Bước 1: Từ một phương trình, biểu diễn một ẩn theo ẩn kia. Ví dụ: từ phương trình \(a_1x + b_1y = c_1\), biểu diễn \(x = \frac{c_1 - b_1y}{a_1}\).
- Bước 2: Thay \(x\) hoặc \(y\) vào phương trình còn lại để tìm ẩn còn lại.
- Bước 3: Thay giá trị của ẩn vừa tìm được vào phương trình đầu tiên để tìm ẩn còn lại.
- Phương pháp cộng đại số:
- Bước 1: Nhân hai phương trình với các hệ số sao cho hệ số của một ẩn giống nhau.
- Bước 2: Cộng hoặc trừ hai phương trình để loại bỏ một ẩn và giải phương trình còn lại.
- Bước 3: Thay giá trị của ẩn vừa tìm được vào một trong hai phương trình ban đầu để tìm ẩn còn lại.
Ví dụ: Giải hệ phương trình sau:
Phương pháp thế:
- Biểu diễn \(x\) từ phương trình thứ hai: \(x = \frac{11 + y}{4}\).
- Thay vào phương trình thứ nhất: \(2\left(\frac{11 + y}{4}\right) + 3y = 5\).
- Giải phương trình: \(5.5 + 0.5y + 3y = 5 \Rightarrow 3.5y = -0.5 \Rightarrow y = -\frac{1}{7}\).
- Thay \(y = -\frac{1}{7}\) vào biểu thức của \(x\): \(x = \frac{11 - \frac{1}{7}}{4} = \frac{77}{28}\).
Dạng bài tập 8: Tính vận tốc trung bình trong chuyển động thẳng
Vận tốc trung bình trong chuyển động thẳng được tính bằng công thức:
Trong đó:
- \(v_{tb}\): Vận tốc trung bình (m/s)
- \(s\): Quãng đường đi được (m)
- \(t\): Thời gian (s)
Để giải bài tập liên quan đến vận tốc trung bình, ta thực hiện các bước sau:
- Bước 1: Xác định quãng đường \(s\) và thời gian \(t\) dựa trên đề bài.
- Bước 2: Áp dụng công thức \(v_{tb} = \frac{s}{t}\) để tính vận tốc trung bình.
- Bước 3: Đơn vị của kết quả phải phù hợp với yêu cầu đề bài (m/s, km/h,...).
Ví dụ: Một người đi quãng đường 120 km trong thời gian 2 giờ. Hãy tính vận tốc trung bình của người đó.
- Giải:
- Quãng đường \(s = 120\) km
- Thời gian \(t = 2\) giờ
- Vận tốc trung bình: \[ v_{tb} = \frac{120}{2} = 60 \, \text{km/h} \]
Vậy vận tốc trung bình của người đó là 60 km/h.
Dạng bài tập 9: Hoàn thành đoạn hội thoại trong Tiếng Anh
Dạng bài tập hoàn thành đoạn hội thoại trong Tiếng Anh thường yêu cầu học sinh điền từ hoặc cụm từ phù hợp vào chỗ trống, giúp đoạn hội thoại trở nên hoàn chỉnh và logic. Để làm dạng bài tập này, ta thực hiện các bước sau:
- Bước 1: Đọc kỹ đoạn hội thoại để nắm bắt ngữ cảnh, chủ đề của cuộc trò chuyện.
- Bước 2: Xác định ngữ pháp và cấu trúc câu phù hợp với chỗ trống cần điền.
- Bước 3: Lựa chọn từ hoặc cụm từ phù hợp với ngữ cảnh, đảm bảo tính logic của cuộc hội thoại.
- Bước 4: Đọc lại toàn bộ đoạn hội thoại sau khi điền để kiểm tra tính mạch lạc và ngữ pháp chính xác.
Ví dụ: Hoàn thành đoạn hội thoại sau:
- A: Hello! How are you today?
- B: I'm fine, thank you. ______?
- A: I'm good too. Have you seen the new movie?
- B: No, I haven't. Is it any good?
Giải:
- Chỗ trống cần điền là câu hỏi xã giao đáp lại lời chào hỏi, câu phù hợp là "And you?"
- Hoàn chỉnh đoạn hội thoại:
- B: I'm fine, thank you. And you?
Vậy, đoạn hội thoại sau khi hoàn chỉnh sẽ có ý nghĩa trôi chảy và tự nhiên.
Dạng bài tập 10: Tính diện tích hình tròn trong Toán học
Trong Toán học, diện tích của hình tròn được tính dựa trên công thức:
Trong đó:
- \(S\) là diện tích của hình tròn.
- \(r\) là bán kính của hình tròn.
- \(\pi\) là hằng số Pi, có giá trị xấp xỉ 3.14159.
Để giải một bài toán tính diện tích hình tròn, ta làm theo các bước sau:
- Bước 1: Xác định bán kính \(r\) của hình tròn.
- Bước 2: Thay giá trị của \(r\) vào công thức \(S = \pi \times r^2\).
- Bước 3: Tính toán giá trị của diện tích \(S\).
Ví dụ: Tính diện tích của một hình tròn có bán kính \(r = 5\) cm.
Giải:
- Sử dụng công thức: \(S = \pi \times r^2 = \pi \times 5^2 = \pi \times 25\).
- Diện tích \(S \approx 3.14159 \times 25 = 78.54\) cm².
Vậy diện tích của hình tròn là \(78.54\) cm².







:max_bytes(150000):strip_icc()/89411-b-complex-vitamins-5b083386ba6177003668e585.png)