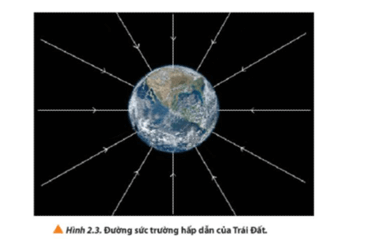
Chủ đề thế hấp dẫn tại một điểm trong trường hấp dẫn: Thế hấp dẫn tại một điểm trong trường hấp dẫn là khái niệm quan trọng trong vật lý học, giải thích về lực hút giữa các vật có khối lượng. Bài viết này sẽ cung cấp kiến thức từ định nghĩa cơ bản đến các công thức và ứng dụng thực tiễn, giúp bạn hiểu rõ về vai trò và tác động của lực hấp dẫn trong vũ trụ.
Mục lục
- Tổng quan về lực hấp dẫn và trường hấp dẫn
- Thế năng hấp dẫn của vật trong trường hấp dẫn
- Thế hấp dẫn tại một điểm và công thức tính toán
- Ứng dụng của thế năng và lực hấp dẫn
- Mối quan hệ giữa thế năng và động năng trong trường hấp dẫn
- Hiện tượng và thí nghiệm liên quan đến lực hấp dẫn
- Ứng dụng của lý thuyết trường hấp dẫn trong thiên văn học
- Kết luận về lý thuyết trường hấp dẫn và ý nghĩa khoa học
Tổng quan về lực hấp dẫn và trường hấp dẫn
Lực hấp dẫn là một trong bốn lực cơ bản của tự nhiên, giữ vai trò quan trọng trong việc cấu thành và duy trì cấu trúc của vũ trụ. Theo định luật vạn vật hấp dẫn của Newton, lực hấp dẫn giữa hai vật tỉ lệ thuận với tích khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng:
Trong đó:
- \(F_{hd}\): Lực hấp dẫn giữa hai vật thể.
- \(G\): Hằng số hấp dẫn, xấp xỉ \(6.67 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2\).
- \(m_1\), \(m_2\): Khối lượng của hai vật thể.
- \(r\): Khoảng cách giữa hai vật thể.
Khái niệm trường hấp dẫn được hình thành nhằm miêu tả không gian xung quanh một vật có khối lượng, trong đó bất kỳ vật nào khác có khối lượng sẽ bị tác động bởi lực hấp dẫn. Trường hấp dẫn tại một điểm được xác định bằng gia tốc trọng trường \(\mathbf{g}\), là lực hấp dẫn tác dụng lên một đơn vị khối lượng đặt tại điểm đó:
Ở đây:
- \(M\): Khối lượng của vật tạo ra trường hấp dẫn.
- \(\mathbf{\hat{r}}\): Vectơ đơn vị hướng từ vật tới điểm cần tính.
Ứng dụng của lực hấp dẫn và trường hấp dẫn
Lực hấp dẫn đóng vai trò quyết định trong chuyển động của các thiên thể trong hệ Mặt Trời, sự hình thành của các hành tinh và các hiện tượng thiên văn khác. Trong khoa học ứng dụng, lực hấp dẫn là cơ sở cho công nghệ định vị vệ tinh GPS, dự đoán quỹ đạo tàu vũ trụ và thậm chí tính toán lực hút trên bề mặt các hành tinh xa xôi.

Thế năng hấp dẫn của vật trong trường hấp dẫn
Thế năng hấp dẫn của một vật là dạng năng lượng tiềm tàng do vị trí của vật trong trường hấp dẫn. Khi một vật có khối lượng \( m \) được đặt tại một độ cao \( h \) so với mặt đất trong trường hấp dẫn của Trái Đất, thế năng hấp dẫn của vật có thể tính bằng công thức:
\[ W_t = m \cdot g \cdot h \]
- m: khối lượng của vật (kg)
- g: gia tốc trọng trường, khoảng \( 9.81 \, \text{m/s}^2 \) trên bề mặt Trái Đất
- h: độ cao của vật so với mốc thế năng (thường là mặt đất)
Như vậy, thế năng hấp dẫn phụ thuộc vào các yếu tố sau:
- Khối lượng của vật: Vật có khối lượng càng lớn sẽ có thế năng hấp dẫn càng cao.
- Gia tốc trọng trường: Thế năng sẽ tăng khi gia tốc trọng trường lớn hơn, ví dụ như trên hành tinh khác.
- Độ cao so với mốc thế năng: Càng cao thì thế năng càng lớn, đại diện cho công cần thiết để di chuyển vật lên độ cao đó.
Thế năng hấp dẫn có thể chuyển hóa thành động năng khi vật chuyển động xuống dưới. Ví dụ, khi thả một viên bi từ độ cao nào đó, thế năng hấp dẫn sẽ biến thành động năng khi viên bi rơi. Ngoài ra, nguyên tắc chuyển hóa này còn có nhiều ứng dụng thực tiễn trong đời sống như:
- Năng lượng thủy điện: Sử dụng thế năng của nước trong các hồ chứa ở vị trí cao để tạo ra điện năng.
- Vệ tinh quay quanh Trái Đất: Sự tương tác giữa thế năng và động năng giúp giữ cho các vệ tinh ở quỹ đạo ổn định.
Nhờ khả năng chuyển hóa và phụ thuộc vào vị trí của vật trong trường hấp dẫn, thế năng hấp dẫn đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và kỹ thuật.
Thế hấp dẫn tại một điểm và công thức tính toán
Trong trường hấp dẫn, thế hấp dẫn tại một điểm là đại lượng quan trọng trong việc nghiên cứu lực hấp dẫn của một vật thể lên các vật thể khác trong không gian xung quanh nó. Thế hấp dẫn có thể được tính toán bằng công thức dựa trên định lý của Newton và lý thuyết trường hấp dẫn.
Để xác định thế hấp dẫn \( V \) tại một điểm cách khối lượng \( M \) một khoảng \( r \), công thức được sử dụng là:
\[
V = - \frac{{G \cdot M}}{{r}}
\]
Trong đó:
- \( G \): hằng số hấp dẫn, có giá trị khoảng \( 6.67430 \times 10^{-11} \, \text{N} \cdot \text{m}^2/\text{kg}^2 \).
- \( M \): khối lượng của vật tạo ra trường hấp dẫn.
- \( r \): khoảng cách từ điểm cần tính đến tâm của vật có khối lượng \( M \).
Thế hấp dẫn thường mang giá trị âm vì theo quy ước, khi một vật di chuyển từ vị trí vô cực (nơi thế hấp dẫn là 0) vào gần khối lượng tạo ra lực hấp dẫn, thế năng của nó giảm đi.
Đặc điểm của thế hấp dẫn là phụ thuộc vào khoảng cách và khối lượng của vật, càng gần vật có khối lượng lớn thì thế năng càng âm, thể hiện lực hút mạnh hơn. Điều này cho phép giải thích nhiều hiện tượng trong thiên văn học, chẳng hạn như sự tồn tại của quỹ đạo hành tinh xung quanh mặt trời và sự tương tác giữa các thiên thể.
| Yếu tố | Ý nghĩa |
|---|---|
| Thế hấp dẫn | Là năng lượng tiềm tàng tại một điểm trong trường hấp dẫn của một vật lớn. |
| Công thức | \( V = - \frac{{G \cdot M}}{{r}} \) |
| Ứng dụng | Giải thích quỹ đạo, chuyển động của hành tinh, và các hiện tượng liên quan trong vũ trụ. |
Hiểu về thế hấp dẫn giúp ta nắm rõ hơn cách mà lực hấp dẫn hoạt động, ảnh hưởng của khối lượng lớn lên không gian xung quanh, từ đó mở rộng hiểu biết về cấu trúc của vũ trụ và các nguyên lý cơ bản trong vật lý thiên văn.
Ứng dụng của thế năng và lực hấp dẫn
Thế năng và lực hấp dẫn có nhiều ứng dụng quan trọng trong cuộc sống và khoa học, từ việc khai thác năng lượng cho đến việc dự đoán và điều khiển quỹ đạo các thiên thể. Dưới đây là một số ứng dụng nổi bật:
- Năng lượng thủy điện: Thế năng hấp dẫn của nước trong các đập cao được chuyển hóa thành động năng khi nước chảy xuống, làm quay các tua-bin để tạo ra điện năng. Đây là nguồn năng lượng tái tạo sạch và hiệu quả.
- Vệ tinh và quỹ đạo: Lực hấp dẫn giúp duy trì quỹ đạo của các vệ tinh quanh Trái Đất. Bằng cách điều chỉnh quỹ đạo dựa vào lực hấp dẫn, các nhà khoa học có thể tính toán chính xác đường đi của vệ tinh cho viễn thông, dự báo thời tiết, và nghiên cứu khí quyển.
- Thám hiểm không gian: Trong hành trình thám hiểm vũ trụ, lực hấp dẫn từ các hành tinh có thể được sử dụng để tăng tốc hoặc thay đổi hướng tàu vũ trụ, gọi là hiệu ứng "trợ lực hấp dẫn". Điều này tiết kiệm năng lượng và chi phí cho các sứ mệnh xa như đến sao Mộc hoặc Sao Thổ.
- Hiểu biết về vũ trụ: Lực hấp dẫn còn giúp các nhà khoa học nghiên cứu cấu trúc và sự tiến hóa của các hệ sao, hành tinh, và thiên hà. Từ đó, chúng ta có thể hiểu rõ hơn về sự hình thành và hoạt động của vũ trụ.
- Ứng dụng trong đời sống hàng ngày: Lực hấp dẫn giữ chúng ta cố định trên mặt đất và hỗ trợ mọi hoạt động từ đi bộ, xây dựng, cho đến giao thông. Mọi vật thể đều bị ảnh hưởng bởi lực hấp dẫn, từ quả táo rơi xuống cho đến chuyển động của máy bay trên bầu trời.
Như vậy, thế năng và lực hấp dẫn đóng vai trò thiết yếu trong cả khoa học và đời sống, không chỉ giúp khai thác nguồn năng lượng sạch mà còn mở ra các hướng nghiên cứu mới về không gian và vật lý học.
Mối quan hệ giữa thế năng và động năng trong trường hấp dẫn
Trong trường hấp dẫn, thế năng và động năng có mối quan hệ chặt chẽ với nhau, thể hiện qua định luật bảo toàn năng lượng. Theo nguyên lý này, tổng cơ năng của một vật sẽ được bảo toàn nếu không có lực bên ngoài tác động. Cụ thể, khi vật di chuyển trong trường hấp dẫn, thế năng và động năng có thể chuyển hóa qua lại nhưng tổng giá trị vẫn không đổi.
1. Thế năng và động năng trong trường hấp dẫn
- Thế năng hấp dẫn \( (U) \): Là dạng năng lượng tiềm năng của vật trong trường hấp dẫn, phụ thuộc vào vị trí của vật so với mặt đất. Công thức tính thế năng hấp dẫn của một vật tại độ cao \( h \) so với mốc thế năng được xác định bởi:
\[
U = m \cdot g \cdot h
\]
trong đó:
- \( m \): khối lượng của vật (kg)
- \( g \): gia tốc trọng trường (m/s²), thường lấy \( g \approx 9.81 \, \text{m/s}^2 \)
- \( h \): độ cao của vật so với mốc thế năng (m)
- Động năng \( (K) \): Là dạng năng lượng của vật khi nó đang chuyển động, được xác định theo công thức:
\[
K = \frac{1}{2}mv^2
\]
trong đó:
- \( m \): khối lượng của vật (kg)
- \( v \): vận tốc của vật (m/s)
2. Sự chuyển hóa giữa thế năng và động năng
Trong quá trình di chuyển dưới tác động của trọng lực, một vật sẽ chuyển hóa thế năng thành động năng khi rơi xuống và ngược lại. Ví dụ, khi một vật được thả từ độ cao nhất định, thế năng sẽ dần giảm đi và chuyển hóa thành động năng, làm cho vận tốc của vật tăng lên. Tại vị trí thấp nhất, toàn bộ thế năng đã chuyển hóa thành động năng.
Công thức tổng quát của sự bảo toàn năng lượng cơ học trong trường hấp dẫn là:
\[
E = U + K
\]
Trong đó:
- \( E \): tổng cơ năng của vật
- \( U \): thế năng hấp dẫn
- \( K \): động năng
3. Ví dụ minh họa
Giả sử một vật có khối lượng \( m = 2 \, \text{kg} \) rơi từ độ cao \( h = 10 \, \text{m} \). Khi vật ở vị trí cao nhất, toàn bộ cơ năng của nó là thế năng:
\[
U = m \cdot g \cdot h = 2 \times 9.81 \times 10 = 196.2 \, \text{J}
\]
Khi vật chạm đất, độ cao \( h = 0 \), do đó \( U = 0 \) và toàn bộ cơ năng đã chuyển thành động năng \( K = 196.2 \, \text{J} \). Điều này minh họa sự bảo toàn năng lượng trong quá trình chuyển động.
Hiện tượng và thí nghiệm liên quan đến lực hấp dẫn
Trong lĩnh vực vật lý, lực hấp dẫn là một hiện tượng cơ bản và đã được nhiều nhà khoa học khám phá qua các thí nghiệm thực tế, nhằm hiểu rõ hơn về cách thức mà lực này ảnh hưởng đến các vật thể trong không gian và trên Trái Đất. Một số hiện tượng tự nhiên, như thủy triều và chuyển động của các hành tinh, là những minh chứng tiêu biểu cho tác động của lực hấp dẫn.
- Thí nghiệm của Galileo: Galileo đã thả hai quả cầu có khối lượng khác nhau từ Tháp Nghiêng Pisa để chứng minh rằng mọi vật đều rơi với gia tốc như nhau trong cùng một trọng trường, bất kể khối lượng của chúng. Điều này góp phần làm sáng tỏ tính chất của lực hấp dẫn và gia tốc trọng trường.
- Thí nghiệm Cavendish: Henry Cavendish là người đầu tiên đo được giá trị của hằng số hấp dẫn, \\( G \\), thông qua thí nghiệm với cân xoắn. Kết quả của ông không chỉ giúp xác định hằng số này mà còn ước tính khối lượng của Trái Đất.
- Thí nghiệm chuyển động của hành tinh: Dựa trên các quy luật của Newton và Kepler, các nhà thiên văn học đã quan sát chuyển động của các hành tinh quanh Mặt Trời. Lực hấp dẫn là yếu tố giúp các hành tinh duy trì quỹ đạo của mình.
Các thí nghiệm này không chỉ làm sáng tỏ về bản chất của lực hấp dẫn mà còn có ý nghĩa sâu sắc trong việc ứng dụng trong công nghệ hiện đại, như định vị GPS và nghiên cứu vũ trụ.
Ứng dụng của lý thuyết trường hấp dẫn trong thiên văn học
Lý thuyết trường hấp dẫn có nhiều ứng dụng quan trọng trong thiên văn học, giúp chúng ta hiểu rõ hơn về cách mà các thiên thể tương tác với nhau trong không gian. Dưới đây là một số ứng dụng tiêu biểu:
- Xác định quỹ đạo của các hành tinh: Lý thuyết trường hấp dẫn được sử dụng để tính toán và dự đoán quỹ đạo của các hành tinh trong hệ Mặt Trời cũng như các hệ sao khác. Bằng cách áp dụng các định luật của Newton, các nhà thiên văn học có thể mô phỏng và theo dõi chuyển động của các hành tinh quanh Mặt Trời.
- Phân tích chuyển động của các ngôi sao: Trong các cụm sao, lý thuyết trường hấp dẫn giúp xác định cách mà các ngôi sao tương tác với nhau, từ đó hiểu được sự hình thành và phát triển của các cụm sao.
- Định vị các vật thể không gian: Các vệ tinh và tàu vũ trụ sử dụng lý thuyết trường hấp dẫn để điều chỉnh quỹ đạo và duy trì vị trí trong không gian, điều này cực kỳ quan trọng cho các nhiệm vụ thám hiểm không gian.
- Nghiên cứu lỗ đen và sóng hấp dẫn: Lý thuyết trường hấp dẫn của Einstein đã mở ra những hiểu biết mới về lỗ đen và sóng hấp dẫn, cho phép các nhà khoa học nghiên cứu và phát hiện ra những hiện tượng cực kỳ phức tạp trong vũ trụ.
Những ứng dụng này không chỉ giúp mở rộng kiến thức của chúng ta về vũ trụ mà còn đóng góp vào các công nghệ hiện đại như GPS và nghiên cứu vũ trụ, tạo ra nhiều cơ hội mới trong nghiên cứu khoa học.

Kết luận về lý thuyết trường hấp dẫn và ý nghĩa khoa học
Lý thuyết trường hấp dẫn là một trong những phát minh vĩ đại nhất trong lịch sử khoa học, mang lại những hiểu biết sâu sắc về lực hấp dẫn và cách mà nó tác động đến mọi vật trong vũ trụ. Từ khi Newton công bố lý thuyết của mình, đến khi Einstein mở rộng nó qua lý thuyết tương đối, chúng ta đã có cái nhìn rõ hơn về các hiện tượng thiên văn, từ chuyển động của các hành tinh đến sự hình thành của lỗ đen.
- Thúc đẩy nghiên cứu khoa học: Lý thuyết này đã mở ra nhiều hướng nghiên cứu mới trong vật lý, thiên văn học và khoa học không gian, tạo điều kiện cho những phát hiện vượt bậc về vũ trụ.
- Ứng dụng công nghệ: Các ứng dụng của lý thuyết trường hấp dẫn trong công nghệ như GPS, vệ tinh và thám hiểm không gian giúp cải thiện đời sống con người và thúc đẩy phát triển kinh tế.
- Khơi gợi sự tò mò và sáng tạo: Lý thuyết trường hấp dẫn không chỉ là một khía cạnh của vật lý mà còn là nguồn cảm hứng cho các nhà khoa học và sinh viên, khuyến khích họ khám phá thêm về vũ trụ và những bí ẩn của nó.
Tóm lại, lý thuyết trường hấp dẫn không chỉ có ý nghĩa quan trọng trong việc giải thích các hiện tượng tự nhiên mà còn là nền tảng cho nhiều tiến bộ trong khoa học và công nghệ, định hình tương lai của nghiên cứu vũ trụ và cuộc sống con người.