Chủ đề video về cường độ trường hấp dẫn: Bài viết giới thiệu về cường độ trường hấp dẫn, một khái niệm cơ bản trong vật lý, giải thích nguyên lý và ứng dụng của nó trong cuộc sống, từ quỹ đạo vệ tinh đến các hiện tượng vũ trụ. Khám phá sâu hơn các công thức và lý thuyết liên quan để hiểu cách trường hấp dẫn ảnh hưởng đến chuyển động và lực trên các hành tinh.
Mục lục
- 1. Giới Thiệu Về Trường Hấp Dẫn
- 2. Khái Niệm Cường Độ Trường Hấp Dẫn
- 3. Lực Hấp Dẫn Trên Các Hành Tinh
- 4. Các Ứng Dụng Của Trường Hấp Dẫn
- 5. Cường Độ Trường Hấp Dẫn Trong Giáo Dục
- 6. Phân Tích Chuyên Sâu Về Công Thức Và Phương Trình Của Trường Hấp Dẫn
- 7. Thế Năng Và Thế Hấp Dẫn
- 8. Định Luật Gauss Cho Trường Hấp Dẫn
- 9. Tổng Kết Và Tài Liệu Tham Khảo
1. Giới Thiệu Về Trường Hấp Dẫn
Trường hấp dẫn là một trong những khái niệm cơ bản của vật lý, thể hiện khả năng của các vật có khối lượng tác dụng lực lên nhau. Khái niệm này được khám phá và phát triển bởi các nhà khoa học từ thời cổ đại, trong đó Isaac Newton là người đặt nền móng với định luật vạn vật hấp dẫn. Theo định luật này, hai vật bất kỳ có khối lượng sẽ hút nhau bằng một lực tỉ lệ thuận với tích khối lượng của chúng và tỉ lệ nghịch với bình phương khoảng cách giữa chúng.
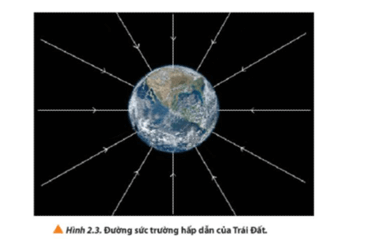
- Định nghĩa trường hấp dẫn: Trường hấp dẫn là khu vực không gian xung quanh một vật có khối lượng mà ở đó vật này tác dụng lực hấp dẫn lên các vật khác. Đối với Trái Đất, trường hấp dẫn của nó là lý do chính làm mọi vật rơi xuống bề mặt trái đất khi không có lực nào khác tác động.
- Tính chất: Trường hấp dẫn có thể coi như một dạng vật chất ảo tồn tại xung quanh một vật có khối lượng, và bất kỳ vật nào trong trường này đều chịu tác dụng của lực hút về phía vật tạo ra trường đó.
- Ứng dụng thực tiễn: Trong cuộc sống và khoa học, trường hấp dẫn có tác động lớn. Ví dụ, hiện tượng thủy triều được tạo ra nhờ tác dụng của trường hấp dẫn từ Mặt Trăng và Mặt Trời lên nước biển của Trái Đất. Điều này ảnh hưởng đến đời sống và môi trường của con người, đặc biệt ở các vùng ven biển.
Trường hấp dẫn không chỉ là lực liên kết các vật thể trong tự nhiên mà còn là nền tảng cho các nghiên cứu về vũ trụ. Các vệ tinh, hành tinh, sao, và thậm chí cả thiên hà đều chịu ảnh hưởng từ trường hấp dẫn, tạo nên các quỹ đạo chuyển động quanh nhau. Đây là yếu tố chủ chốt giúp các nhà thiên văn học nghiên cứu sự hình thành và phát triển của các thiên thể trong vũ trụ.
- Tác động của trường hấp dẫn trong vũ trụ: Từ các ngôi sao đến hành tinh và thiên hà, mọi thiên thể đều liên kết với nhau thông qua trường hấp dẫn, giúp duy trì trật tự và các quỹ đạo ổn định. Ví dụ, Trái Đất quay quanh Mặt Trời là nhờ lực hấp dẫn của Mặt Trời.
- Vai trò trong nghiên cứu khoa học: Nghiên cứu trường hấp dẫn không chỉ giúp hiểu sâu hơn về sự chuyển động của các hành tinh mà còn ứng dụng trong việc phóng vệ tinh và thăm dò vũ trụ. Hiểu rõ trường hấp dẫn còn hỗ trợ tính toán quỹ đạo của các tàu vũ trụ và vệ tinh một cách chính xác.
Trường hấp dẫn không chỉ dừng lại ở lý thuyết mà còn có nhiều ứng dụng quan trọng trong các lĩnh vực như hàng không, vũ trụ và địa vật lý. Từ việc tính toán lực hút của Trái Đất để thiết kế tàu vũ trụ đến các nghiên cứu ảnh hưởng của trọng lực lên sức khỏe con người trong môi trường không trọng lực, tất cả đều góp phần phát triển khoa học và công nghệ không gian.

2. Khái Niệm Cường Độ Trường Hấp Dẫn
Cường độ trường hấp dẫn là một đại lượng đặc trưng cho trường hấp dẫn, thể hiện khả năng tác động lực của một vật có khối lượng lớn lên các vật khác nằm trong trường hấp dẫn của nó. Tại bất kỳ điểm nào trong trường này, cường độ trường hấp dẫn phụ thuộc vào khối lượng của vật tạo ra trường và khoảng cách từ điểm đó đến vật.
Công thức để tính cường độ trường hấp dẫn tại một điểm cách xa một vật cầu đồng chất với khối lượng \( M \) là:
\[ g = \frac{G \cdot M}{r^2} \]
trong đó:
- \( g \): Cường độ trường hấp dẫn (đơn vị m/s2), tương đương với gia tốc trọng trường.
- \( G \): Hằng số hấp dẫn với giá trị khoảng \( 6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2 \).
- \( M \): Khối lượng của vật tạo ra trường (kg).
- \( r \): Khoảng cách từ tâm của vật đến điểm cần tính (m).
Điều này có nghĩa là cường độ trường hấp dẫn tỷ lệ thuận với khối lượng của vật và tỷ lệ nghịch với bình phương khoảng cách đến vật đó. Vì vậy, khi khoảng cách tăng lên, cường độ trường giảm mạnh. Tại bề mặt Trái Đất, cường độ trường hấp dẫn trung bình là khoảng 9.8 m/s2.
Các đặc điểm quan trọng của cường độ trường hấp dẫn:
- Phụ thuộc vào khoảng cách: Càng xa vật tạo ra trường, cường độ càng nhỏ, theo tỉ lệ nghịch với bình phương khoảng cách.
- Không phụ thuộc vào khối lượng của vật chịu tác dụng: Cường độ trường chỉ phụ thuộc vào vật tạo ra trường và khoảng cách, không phụ thuộc vào khối lượng của vật đặt trong trường.
Cường độ trường hấp dẫn là nền tảng cho việc xác định lực hấp dẫn mà các hành tinh, sao và các vật thể thiên văn khác tác động lên nhau, giúp hiểu rõ hơn về cách vũ trụ được kết nối qua lực hấp dẫn.
3. Lực Hấp Dẫn Trên Các Hành Tinh
Lực hấp dẫn trên các hành tinh khác nhau trong Hệ Mặt Trời được xác định dựa trên khối lượng và bán kính của chúng. Vì mỗi hành tinh có mật độ và cấu trúc khác nhau, lực hấp dẫn tại bề mặt cũng có sự biến đổi rõ rệt, từ đó ảnh hưởng đến môi trường và điều kiện sống giả định nếu con người khám phá không gian.
3.1 So Sánh Cường Độ Trường Hấp Dẫn Của Trái Đất Và Mặt Trăng
Lực hấp dẫn trên Mặt Trăng nhỏ hơn Trái Đất rất nhiều, chỉ khoảng 0,1654 lần so với trọng lực tại Trái Đất. Điều này có nghĩa là các vật thể trên Mặt Trăng sẽ nhẹ hơn, và các phi hành gia có thể nhảy cao hơn hoặc di chuyển dễ dàng hơn so với trên Trái Đất. Điều kiện trọng lực này mang lại những lợi ích cho việc thí nghiệm khoa học, nhưng cũng đòi hỏi con người phải thích nghi nếu muốn thực hiện các hoạt động dài hạn.
3.2 Ứng Dụng Trong Tính Toán Lực Hấp Dẫn Trên Các Hành Tinh Khác
Mỗi hành tinh trong Hệ Mặt Trời có cường độ trường hấp dẫn riêng biệt:
- Sao Thủy: Lực hấp dẫn chỉ khoảng 0,38 lần so với Trái Đất, cho thấy trọng lực rất yếu.
- Sao Kim: Có lực hấp dẫn tương đương 0,9 lần Trái Đất, làm cho nó trở thành một điểm nghiên cứu tiềm năng cho khoa học không gian.
- Sao Hỏa: Với lực hấp dẫn xấp xỉ 0,38 lần so với Trái Đất, tạo điều kiện để con người có thể đi lại dễ dàng hơn, nhưng cần các biện pháp thích nghi.
- Sao Mộc: Đây là hành tinh có lực hấp dẫn mạnh nhất trong Hệ Mặt Trời, khoảng 2,528 lần so với Trái Đất. Tuy nhiên, sao Mộc không có bề mặt rắn, nên việc nghiên cứu phải thực hiện trên các đám mây bao quanh.
- Sao Thổ: Cũng là một hành tinh khí khổng lồ với lực hấp dẫn khoảng 1,065 lần trọng lực Trái Đất, chủ yếu tập trung trên bề mặt các tầng mây.
- Sao Thiên Vương và Sao Hải Vương: Lực hấp dẫn tương ứng là 0,886 và 1,14 lần trọng lực của Trái Đất, với cấu trúc khí khiến việc tiếp cận và nghiên cứu gặp thách thức.
Các số liệu về lực hấp dẫn này không chỉ giúp chúng ta hiểu rõ hơn về sự đa dạng của các hành tinh mà còn là cơ sở để chuẩn bị cho những chuyến thám hiểm trong tương lai. Nhờ đó, các phi hành gia có thể dự đoán cách mà trọng lực sẽ ảnh hưởng đến cơ thể và trang thiết bị, từ đó có kế hoạch thích nghi phù hợp.
4. Các Ứng Dụng Của Trường Hấp Dẫn
Trường hấp dẫn đóng vai trò quan trọng trong nhiều lĩnh vực khoa học và đời sống. Các ứng dụng của trường hấp dẫn giúp con người hiểu và khai thác nhiều hiện tượng trong vũ trụ, phát triển công nghệ vũ trụ và hỗ trợ nghiên cứu khoa học hành tinh. Dưới đây là một số ứng dụng nổi bật của trường hấp dẫn:
- Vai Trò Của Trường Hấp Dẫn Trong Vũ Trụ
Trường hấp dẫn là yếu tố chính giúp các hành tinh duy trì quỹ đạo của chúng quanh Mặt Trời. Lực hấp dẫn do các hành tinh lớn tạo ra còn ảnh hưởng đến sự hình thành quỹ đạo của các tiểu hành tinh và vệ tinh tự nhiên. Mặt Trời nhờ vào trường hấp dẫn đã tạo ra hệ mặt trời ổn định với quỹ đạo của các hành tinh và các thiên thể nhỏ.
- Ứng Dụng Trong Khoa Học Vũ Trụ Và Công Nghệ Không Gian
Công nghệ vũ trụ như vệ tinh nhân tạo và các tàu thăm dò phụ thuộc vào hiểu biết về trường hấp dẫn để điều chỉnh quỹ đạo và vị trí. Trường hấp dẫn của Trái Đất giúp giữ vệ tinh trong quỹ đạo, cung cấp nền tảng cho các dịch vụ như định vị GPS và viễn thông.
Đồng thời, các nghiên cứu sử dụng "hiệu ứng trường hấp dẫn" còn giúp tính toán hành trình và tăng tốc của các tàu thăm dò, như tàu Voyager hay tàu thăm dò tới Sao Mộc, nhờ vào lực hấp dẫn của các hành tinh lớn để thay đổi hướng di chuyển mà không cần dùng nhiều nhiên liệu.
- Cường Độ Trường Hấp Dẫn Trong Nghiên Cứu Hành Tinh
Trong nghiên cứu địa chất, cường độ trường hấp dẫn được ứng dụng để phân tích cấu trúc của Trái Đất và các hành tinh khác. Bằng cách đo đạc sự biến đổi của cường độ trường hấp dẫn, các nhà khoa học có thể phát hiện các bất thường dưới bề mặt như khoáng sản, dầu khí hoặc cấu trúc địa chất của hành tinh.
Trường hấp dẫn không chỉ có vai trò trong nghiên cứu khoa học mà còn cung cấp nền tảng cho nhiều công nghệ thiết yếu trong cuộc sống hàng ngày, từ truyền thông đến điều hướng toàn cầu, giúp con người khai thác tối đa tiềm năng của không gian và vũ trụ.

5. Cường Độ Trường Hấp Dẫn Trong Giáo Dục
Cường độ trường hấp dẫn là một nội dung quan trọng trong chương trình Vật lý ở cấp trung học phổ thông, giúp học sinh hiểu sâu hơn về các khái niệm liên quan đến lực hấp dẫn và các ứng dụng thực tiễn của nó. Nội dung này không chỉ cung cấp kiến thức lý thuyết mà còn phát triển năng lực tư duy, tự học và khả năng vận dụng kiến thức vào thực tế.
5.1 Giới Thiệu Bài Học Về Trường Hấp Dẫn Trong Chương Trình Lớp 11
Trong chương trình Vật lý lớp 11, học sinh được tiếp cận với khái niệm và định nghĩa của cường độ trường hấp dẫn. Bài học này bao gồm:
- Khái niệm cơ bản: Cường độ trường hấp dẫn được định nghĩa là lực tác dụng lên một đơn vị khối lượng tại một điểm trong trường hấp dẫn, ký hiệu là g.
- Công thức tính toán: Cường độ trường hấp dẫn tại một điểm cách tâm của vật khối lượng M một khoảng r được tính bằng công thức: \( g = \frac{GM}{r^2} \)
- Phân tích qua thực nghiệm: Học sinh được hướng dẫn thực hiện các bài tập và thí nghiệm đơn giản nhằm củng cố hiểu biết về cường độ trường hấp dẫn gần mặt đất.
5.2 Thảo Luận Và Bài Tập Về Cường Độ Trường Hấp Dẫn
Học sinh tham gia các bài tập và thảo luận theo nhóm để mở rộng kiến thức và hiểu sâu hơn về cường độ trường hấp dẫn, bao gồm:
- Thảo luận về cách lực hấp dẫn thay đổi khi thay đổi khoảng cách giữa các vật thể và ứng dụng thực tế của điều này.
- Thực hành tính toán cường độ trường hấp dẫn của Trái Đất và các hành tinh khác trong hệ Mặt Trời.
- Phân tích sự khác biệt giữa trọng lực và cường độ trường hấp dẫn trong các môi trường khác nhau.
5.3 Giáo Án Và Tài Liệu Học Tập Cho Giáo Viên
Để hỗ trợ giáo viên giảng dạy về cường độ trường hấp dẫn, nhiều tài liệu và giáo án chuyên sâu đã được cung cấp, bao gồm:
- Giáo án điện tử và video hướng dẫn: Các tài liệu đa phương tiện giúp học sinh dễ dàng hình dung và hiểu rõ hơn về trường hấp dẫn.
- Hoạt động thực nghiệm: Thực hiện các bài thí nghiệm với mô hình đơn giản để minh họa tác động của cường độ trường hấp dẫn lên các vật thể.
- Bài kiểm tra đánh giá năng lực: Các bài kiểm tra đánh giá mức độ hiểu biết của học sinh về cường độ trường và lực hấp dẫn, giúp giáo viên điều chỉnh phương pháp giảng dạy phù hợp.
Qua các nội dung này, học sinh không chỉ nắm vững kiến thức lý thuyết mà còn phát triển năng lực tư duy logic, khả năng giải quyết vấn đề và tự học.
6. Phân Tích Chuyên Sâu Về Công Thức Và Phương Trình Của Trường Hấp Dẫn
Trong vật lý, trường hấp dẫn và cường độ của nó được mô tả qua các công thức và phương trình, giúp chúng ta hiểu cách lực hấp dẫn hoạt động và ảnh hưởng đến vật thể có khối lượng. Sau đây là phân tích chuyên sâu về công thức và phương trình liên quan đến trường hấp dẫn:
6.1 Phương Trình Lực Hấp Dẫn Theo Định Luật Vạn Vật Hấp Dẫn Của Newton
Định luật vạn vật hấp dẫn của Newton phát biểu rằng lực hấp dẫn giữa hai vật có khối lượng \( m_1 \) và \( m_2 \) cách nhau một khoảng \( r \) được tính bằng công thức:
\[ F = G \frac{{m_1 \cdot m_2}}{{r^2}} \]
Trong đó:
- \( F \): Lực hấp dẫn giữa hai vật (N)
- \( G \): Hằng số hấp dẫn, khoảng \(6.674 \times 10^{-11} \, \text{N} \cdot \text{m}^2/\text{kg}^2\)
- \( m_1 \) và \( m_2 \): Khối lượng của hai vật (kg)
- \( r \): Khoảng cách giữa hai vật (m)
6.2 Phương Trình Cường Độ Trường Hấp Dẫn
Cường độ trường hấp dẫn \( g \) tại một điểm trong trường hấp dẫn do vật có khối lượng \( M \) tạo ra, cách vật một khoảng \( r \), được xác định bằng:
\[ g = G \frac{M}{r^2} \]
Trong đó:
- \( g \): Cường độ trường hấp dẫn (m/s²)
- \( M \): Khối lượng của vật tạo ra trường hấp dẫn (kg)
- \( r \): Khoảng cách từ tâm vật đến điểm xét (m)
Phương trình này chỉ ra rằng cường độ trường hấp dẫn tỉ lệ nghịch với bình phương khoảng cách \( r \). Điều này có nghĩa là càng xa vật tạo trường thì cường độ trường hấp dẫn càng nhỏ.
6.3 Sử Dụng Phương Trình Để Giải Bài Tập Thực Tế
Để áp dụng công thức này vào bài tập thực tế, chúng ta có thể tính lực hấp dẫn hoặc cường độ trường hấp dẫn tại bề mặt Trái Đất hoặc một điểm cụ thể trên bề mặt các hành tinh khác. Ví dụ:
- Tính cường độ trường hấp dẫn tại bề mặt Trái Đất: Với khối lượng của Trái Đất là \( 5.97 \times 10^{24} \, \text{kg} \) và bán kính khoảng \( 6,371 \, \text{km} \), ta có thể áp dụng công thức để tính \( g \) tại bề mặt Trái Đất.
- Tính lực hấp dẫn giữa Trái Đất và Mặt Trăng: Dựa vào khoảng cách trung bình và khối lượng của cả hai, sử dụng công thức lực hấp dẫn của Newton để tính toán.
Phương trình và phương pháp tính này còn được áp dụng rộng rãi trong nghiên cứu khoa học vũ trụ, giúp xác định cách các hành tinh và thiên thể tác động lẫn nhau qua lực hấp dẫn.
Kết luận, hiểu và áp dụng các phương trình của trường hấp dẫn là nền tảng cho nhiều lĩnh vực nghiên cứu về vật lý thiên văn và cơ học, giúp chúng ta khám phá sâu hơn về vũ trụ và tương tác giữa các thiên thể.
7. Thế Năng Và Thế Hấp Dẫn
Thế năng và thế hấp dẫn là những khái niệm quan trọng trong vật lý, liên quan đến lực hấp dẫn và năng lượng của các vật thể trong trường hấp dẫn.
7.1 Khái Niệm Thế Năng Hấp Dẫn
Thế năng hấp dẫn của một vật thể là năng lượng tiềm tàng của nó, phát sinh từ tương tác giữa vật thể với Trái Đất hoặc một hành tinh khác. Nó phụ thuộc vào vị trí của vật trong trọng trường, đặc biệt là độ cao so với một mốc được chọn, thường là mặt đất.
- Thế năng được tính bằng công thức: \( W_t = m \cdot g \cdot h \)
- Trong đó:
- \( m \): khối lượng của vật (kg)
- \( g \): gia tốc trọng trường, khoảng \( 9.8 \, m/s^2 \) trên Trái Đất
- \( h \): độ cao của vật so với mốc thế năng (m)
7.2 Thế Hấp Dẫn Của Một Vật Trong Trường Hấp Dẫn
Đối với hai vật có khối lượng lớn, công thức tổng quát hơn của thế năng hấp dẫn được sử dụng:
- \( U = -\frac{G \cdot M \cdot m}{R} \)
- Trong đó:
- \( G \): hằng số hấp dẫn (\(6.67430 \times 10^{-11} \, m^3/kg/s^2\))
- \( M \) và \( m \): khối lượng của hai vật thể (kg)
- \( R \): khoảng cách giữa tâm của hai vật thể (m)
Giá trị của \( U \) có thể dương hoặc âm, tùy thuộc vào vị trí mốc thế năng được chọn.
7.3 Ứng Dụng Thế Năng Trong Tính Toán Lực Hấp Dẫn
Thế năng hấp dẫn có nhiều ứng dụng thực tiễn trong khoa học và đời sống:
- Trong Khoa Học: Thế năng hấp dẫn được sử dụng để nghiên cứu quỹ đạo hành tinh, sự tương tác giữa các thiên thể và tính toán chuyển động của các vật thể trong vũ trụ.
- Trong Công Nghệ: Thế năng được ứng dụng trong việc xây dựng các hệ thống thủy điện và các cấu trúc phụ thuộc vào lực hấp dẫn.
- Trong Đời Sống: Thế năng hấp dẫn được khai thác trong các môn thể thao mạo hiểm như nhảy dù và trượt tuyết.
Nhờ thế năng và lực hấp dẫn, chúng ta có thể tính toán và điều chỉnh năng lượng của các vật thể trong các hệ thống vật lý thực tế, từ đó ứng dụng vào việc dự đoán và điều khiển chuyển động của vệ tinh và tàu vũ trụ.

8. Định Luật Gauss Cho Trường Hấp Dẫn
Định luật Gauss là một công cụ quan trọng trong vật lý, giúp phân tích trường hấp dẫn thông qua sự phân bố của khối lượng và cường độ trường. Đối với trường hấp dẫn, định luật Gauss phát biểu rằng:
\[
\Phi_G = \oint_{S} \mathbf{G} \cdot d\mathbf{A} = -4 \pi G M
\]
Trong đó:
- \(\Phi_G\) là thông lượng hấp dẫn qua mặt kín \(S\),
- \(\mathbf{G}\) là cường độ trường hấp dẫn tại một điểm trên bề mặt,
- \(d\mathbf{A}\) là một phần tử diện tích vi phân trên bề mặt Gauss,
- \(G\) là hằng số hấp dẫn (khoảng \(6.67 \times 10^{-11}\) Nm2/kg2),
- \(M\) là tổng khối lượng bên trong bề mặt Gauss.
Trong thực tế, định luật Gauss giúp đơn giản hóa các phép tính đối với trường hấp dẫn quanh các vật thể có tính đối xứng, như khối cầu hoặc hình cầu rỗng, bằng cách lựa chọn mặt Gauss thích hợp. Với một vật thể có tính đối xứng cầu, mặt Gauss là một mặt cầu đồng tâm với vật thể, từ đó:
\[
G(r) = \frac{GM}{r^2}
\]
với \(r\) là khoảng cách từ tâm của khối lượng \(M\) đến điểm cần tính trường. Điều này cho phép suy ra trường hấp dẫn xung quanh các thiên thể như hành tinh và sao.
Các Bước Sử Dụng Định Luật Gauss Trong Tính Toán
- Xác định mặt Gauss: Chọn mặt Gauss thích hợp (thường là hình cầu) bao quanh khối lượng cần tính toán.
- Tính toán thông lượng hấp dẫn: Sử dụng tích phân bề mặt để tính toán \(\Phi_G\).
- Áp dụng công thức: Sử dụng \(\Phi_G = -4 \pi G M\) để tìm ra cường độ trường tại các điểm trên mặt Gauss.
Định luật Gauss cho trường hấp dẫn không chỉ hữu ích trong nghiên cứu thiên văn mà còn được áp dụng trong các bài toán thực tế như tính toán trọng lực của các hành tinh và các ngôi sao xa xôi.
9. Tổng Kết Và Tài Liệu Tham Khảo
Qua các nội dung trên, chúng ta đã tìm hiểu sâu sắc về trường hấp dẫn, từ khái niệm cơ bản, cường độ trường, công thức tính toán đến các ứng dụng rộng rãi trong thực tiễn và nghiên cứu khoa học. Trường hấp dẫn không chỉ ảnh hưởng đến các hiện tượng tự nhiên như sự quay quanh mặt trời của các hành tinh mà còn đóng vai trò quan trọng trong việc nghiên cứu và phát triển các công nghệ không gian.
9.1 Tổng Kết Kiến Thức
- Trường hấp dẫn: Là trường vật lý được tạo ra xung quanh một vật có khối lượng, có khả năng tác động lực hấp dẫn lên các vật khác.
- Cường độ trường hấp dẫn: Được xác định thông qua công thức \( g = \frac{GM}{r^2} \), thể hiện khả năng tác động lực của một vật có khối lượng \( M \) tại khoảng cách \( r \).
- Định luật Gauss cho trường hấp dẫn: Giúp xác định cách tính cường độ trường trong các trường hợp có sự đối xứng như các vật thể hình cầu.
- Ứng dụng thực tiễn: Trường hấp dẫn có ứng dụng quan trọng trong việc giải thích các hiện tượng thiên văn và hỗ trợ trong ngành công nghệ không gian.
9.2 Các Video Hướng Dẫn Và Tài Liệu Tự Học
Các video học tập và tài liệu sau sẽ hỗ trợ quá trình ôn tập và tìm hiểu sâu hơn:
9.3 Thư Viện Tài Liệu Tham Khảo Thêm
| Tài Liệu | Nội Dung |
|---|---|
| Giáo trình Vật Lý 11 - Kết Nối Tri Thức | Hệ thống lý thuyết và bài tập về trường và lực hấp dẫn, cường độ trường và thế năng hấp dẫn. |
| Sách tham khảo: "Vật Lý Thiên Văn" | Giới thiệu về vai trò của trường hấp dẫn trong vũ trụ học và các hiện tượng thiên văn. |
| Tài liệu trực tuyến tại Hocmai | Khóa học, video, và bài tập thực hành từ các chủ đề vật lý liên quan đến trường hấp dẫn. |
Hy vọng rằng, với những kiến thức và tài liệu tham khảo này, bạn sẽ có nền tảng vững chắc để hiểu rõ hơn về trường hấp dẫn và cường độ của nó, cũng như cách áp dụng vào các hiện tượng tự nhiên và thực tế trong khoa học và công nghệ hiện đại.