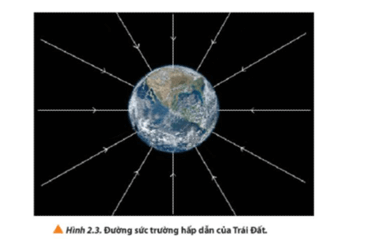
Chủ đề bài 3 cường độ trường hấp dẫn: Bài viết này trình bày chi tiết về cường độ trường hấp dẫn - một đại lượng quan trọng trong vật lý, giúp đo lường lực hấp dẫn tác động lên vật thể tại một điểm trong không gian. Với các khái niệm cơ bản, công thức tính toán cùng ứng dụng thực tế trong thiên văn và khoa học vũ trụ, bài viết sẽ cung cấp nền tảng kiến thức cần thiết để học sinh và người đọc hiểu rõ bản chất và ý nghĩa của trường hấp dẫn trong môi trường học tập và nghiên cứu.
Mục lục
Khái niệm về cường độ trường hấp dẫn
Cường độ trường hấp dẫn là đại lượng mô tả đặc trưng của trường hấp dẫn về khả năng tác dụng lực của nó lên một vật có khối lượng bất kỳ đặt trong trường. Theo lý thuyết trường hấp dẫn, cường độ trường tại một điểm trong không gian xung quanh một vật có khối lượng lớn (ví dụ như Trái Đất) cho biết lực mà trường hấp dẫn này sẽ tác dụng lên mỗi đơn vị khối lượng tại điểm đó.
Đơn vị đo của cường độ trường hấp dẫn là Newton trên kilogram (\(N/kg\)), thường ký hiệu là \(g\) hoặc \(G\) khi tính theo định luật vạn vật hấp dẫn. Công thức chung để tính cường độ trường hấp dẫn \(g\) ở một điểm cách vật sinh ra lực một khoảng \(r\) có dạng:
\[
g = \dfrac{G \cdot M}{r^2}
\]
Trong đó:
- \(G\) là hằng số hấp dẫn, có giá trị xấp xỉ \(6.674 \times 10^{-11} \, m^3 kg^{-1} s^{-2}\).
- \(M\) là khối lượng của vật tạo ra trường hấp dẫn, thường là Trái Đất hay một thiên thể khác.
- \(r\) là khoảng cách từ tâm của vật tạo ra lực đến điểm cần tính cường độ trường hấp dẫn.
Công thức trên cho thấy cường độ trường hấp dẫn giảm dần khi khoảng cách \(r\) tăng lên, phù hợp với định luật bình phương nghịch đảo. Đối với Trái Đất, cường độ trường hấp dẫn trên bề mặt trung bình khoảng \(9.81 \, N/kg\), nhưng giá trị này có thể thay đổi một chút tùy thuộc vào độ cao và vị trí địa lý cụ thể.
Điều này có ý nghĩa rằng tại mỗi điểm trong trường hấp dẫn của Trái Đất, một vật sẽ chịu một lực tác dụng tỷ lệ thuận với khối lượng của nó. Ví dụ, nếu một vật có khối lượng 10 kg, lực hấp dẫn tác dụng lên nó tại bề mặt Trái Đất là:
\[
F = m \cdot g = 10 \, kg \times 9.81 \, N/kg = 98.1 \, N
\]
Nhờ việc hiểu rõ về khái niệm và cách tính cường độ trường hấp dẫn, chúng ta có thể dự đoán các lực tác động lên các vật trong không gian gần các thiên thể lớn, giúp ích cho các nghiên cứu khoa học và ứng dụng thực tiễn như trong việc phóng vệ tinh và các nhiệm vụ không gian khác.

Công thức tính cường độ trường hấp dẫn
Trong vật lý, công thức tính cường độ trường hấp dẫn mô tả lực hấp dẫn mà một vật thể tạo ra ở một điểm cụ thể trong không gian. Công thức này liên quan đến khối lượng của vật và khoảng cách từ vật đó tới điểm mà chúng ta đo lường cường độ trường hấp dẫn.
Cường độ trường hấp dẫn \(g\) tại một điểm cách xa tâm của vật thể khối lượng \(M\) một khoảng \(r\) được tính bằng công thức:
- \[ g = G \frac{M}{r^2} \]
Trong đó:
- G là hằng số hấp dẫn với giá trị xấp xỉ \(6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2\).
- M là khối lượng của vật tạo ra lực hấp dẫn, thường là một thiên thể như Trái Đất hay Mặt Trời.
- r là khoảng cách từ tâm vật đến điểm cần tính cường độ trường hấp dẫn.
Ví dụ, cường độ trường hấp dẫn của Trái Đất tại mặt đất được tính với bán kính Trái Đất \(R_{TD} \approx 6.371 \times 10^6 \, \text{m}\) và khối lượng Trái Đất \(M_{TD} \approx 5.972 \times 10^{24} \, \text{kg}\), từ đó:
- \[ g = 6.674 \times 10^{-11} \times \frac{5.972 \times 10^{24}}{(6.371 \times 10^6)^2} \approx 9.8 \, \text{m/s}^2 \]
Giá trị này cho thấy cường độ trường hấp dẫn gần bề mặt Trái Đất là xấp xỉ \(9.8 \, \text{m/s}^2\), nghĩa là mỗi kg khối lượng sẽ chịu một lực hút khoảng \(9.8 \, \text{N}\).
Khi di chuyển ra xa, như lên độ cao lớn hoặc vào không gian, giá trị \(r\) tăng lên, và do đó, cường độ trường hấp dẫn giảm theo công thức trên. Điều này giải thích tại sao lực hấp dẫn yếu đi khi ra xa khỏi bề mặt Trái Đất.
So sánh cường độ trường hấp dẫn của Trái Đất và các thiên thể khác
Cường độ trường hấp dẫn của Trái Đất và các thiên thể khác nhau trong Hệ Mặt Trời có sự chênh lệch lớn, phụ thuộc vào khối lượng và kích thước của từng thiên thể. Dưới đây là phân tích chi tiết cường độ trường hấp dẫn của Trái Đất so với một số hành tinh và Mặt Trăng:
- Trái Đất: Cường độ trường hấp dẫn tại bề mặt của Trái Đất là 9,81 m/s², tương đương với 1 g. Đây là mức cường độ mà chúng ta cảm nhận được và đã quen thuộc trong môi trường sống hàng ngày.
- Mặt Trăng: Với khối lượng nhỏ hơn Trái Đất, cường độ trường hấp dẫn trên Mặt Trăng là khoảng 1,62 m/s², chỉ bằng 17% so với Trái Đất. Điều này giải thích tại sao các phi hành gia có thể nhảy cao và di chuyển dễ dàng hơn trên Mặt Trăng.
- Sao Hỏa: Lực hấp dẫn trên sao Hỏa là 3,71 m/s², bằng 0,38 g của Trái Đất. Với lực hấp dẫn thấp hơn, một người nặng 100 kg trên Trái Đất sẽ chỉ nặng khoảng 38 kg trên sao Hỏa.
- Sao Mộc: Là hành tinh có khối lượng lớn nhất trong Hệ Mặt Trời, sao Mộc có cường độ trường hấp dẫn lên đến 24,79 m/s² (tương đương 2,528 g). Tuy nhiên, do bản chất khí khổng lồ, không có bề mặt rắn mà con người có thể đứng vững.
- Sao Thổ: Dù kích thước rất lớn, cường độ trường hấp dẫn của sao Thổ là 10,44 m/s² (1,065 g), không quá lớn do mật độ thấp.
- Sao Thiên Vương và Sao Hải Vương: Lực hấp dẫn của các hành tinh này lần lượt là 8,69 m/s² và 11,15 m/s², thấp hơn Trái Đất nhưng cũng đủ lớn để tạo thành các hành tinh khí khổng lồ ổn định.
Nhìn chung, cường độ trường hấp dẫn tại bề mặt của các hành tinh phụ thuộc chủ yếu vào khối lượng và bán kính của chúng. Những hành tinh có khối lượng lớn như sao Mộc hay sao Thổ sẽ có lực hấp dẫn mạnh hơn, trong khi những thiên thể nhỏ hơn như Mặt Trăng hay sao Hỏa có lực hấp dẫn yếu hơn nhiều.
Vận dụng cường độ trường hấp dẫn trong giải bài tập
Việc hiểu rõ cường độ trường hấp dẫn và các công thức liên quan giúp học sinh có thể áp dụng chính xác trong các bài tập tính toán thực tế. Dưới đây là một số bước cơ bản khi vận dụng cường độ trường hấp dẫn để giải quyết các bài toán:
- Nhận diện và xác định các thông số cần thiết: Đầu tiên, cần đọc kỹ bài tập và xác định các thông số đã cho như khối lượng \( M \), bán kính \( R \) của thiên thể, hoặc khoảng cách giữa hai vật thể. Các thông số này là cơ sở để áp dụng công thức tính cường độ trường hấp dẫn.
- Áp dụng công thức tính cường độ trường hấp dẫn: Công thức chuẩn để tính cường độ trường hấp dẫn tại một điểm cách khối tâm của vật thể một khoảng \( r \) là: \[ g = \frac{{G \cdot M}}{{r^2}} \] với \( G \) là hằng số hấp dẫn (khoảng \( 6.67 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2 \)), \( M \) là khối lượng của thiên thể và \( r \) là khoảng cách từ tâm đến vị trí đang xét.
- Tính toán và so sánh kết quả: Sau khi tính toán giá trị \( g \), có thể so sánh kết quả này với các hành tinh hoặc thiên thể khác để đánh giá sự khác biệt trong cường độ trường hấp dẫn.
- Ứng dụng trong các bài toán thực tế: Trong các bài toán, học sinh có thể sử dụng cường độ trường hấp dẫn để tính trọng lực tác động lên vật có khối lượng \( m \) ở một vị trí xác định với công thức \( F = m \cdot g \). Đây là ứng dụng quan trọng trong nhiều bài tập cơ bản.
Việc thực hành giải các bài tập vận dụng cường độ trường hấp dẫn giúp củng cố kiến thức, đồng thời tăng khả năng tư duy và kỹ năng toán học khi xử lý các đại lượng vật lý phức tạp.
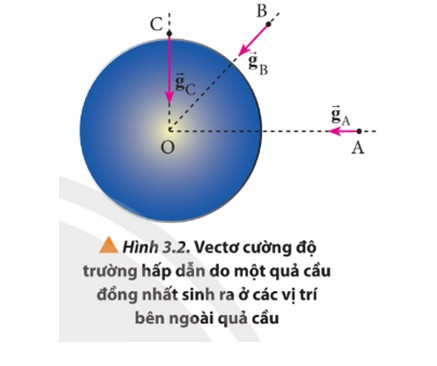
Các hiện tượng vật lý liên quan đến trường hấp dẫn
Trường hấp dẫn là một trong những yếu tố then chốt trong việc nghiên cứu các hiện tượng tự nhiên trên Trái Đất cũng như trong vũ trụ. Dưới đây là một số hiện tượng vật lý điển hình có liên quan trực tiếp đến trường hấp dẫn:
Hiện tượng rơi tự do và gia tốc trọng trường
Khi một vật rơi tự do từ độ cao xuống mặt đất, nó chịu tác động của lực hấp dẫn từ Trái Đất. Lực này làm cho vật tăng tốc đều đặn với gia tốc trọng trường \( g \approx 9,8 \, \text{m/s}^2 \) (gần mặt đất). Gia tốc trọng trường này là một hệ quả trực tiếp của cường độ trường hấp dẫn và phụ thuộc vào khoảng cách từ vật đến tâm Trái Đất.
Hiện tượng không trọng lượng trên trạm vũ trụ ISS
Trên trạm vũ trụ quốc tế ISS, mặc dù các phi hành gia và trạm ISS vẫn chịu tác dụng của lực hấp dẫn từ Trái Đất, nhưng do ISS di chuyển với vận tốc lớn theo quỹ đạo quanh Trái Đất nên trạng thái "rơi tự do" liên tục của ISS tạo cảm giác không trọng lượng cho các phi hành gia. Điều này cho phép họ thực hiện các thí nghiệm trong môi trường không trọng lượng để nghiên cứu tác động của trọng lực lên cơ thể và các vật thể.
Ứng dụng của trường hấp dẫn trong nghiên cứu thiên văn học
- Hiện tượng thủy triều: Sự tác động đồng thời của lực hấp dẫn từ Mặt Trăng và Mặt Trời lên Trái Đất tạo ra hiện tượng thủy triều. Lực hấp dẫn làm cho nước biển dâng cao hoặc hạ thấp tại các vị trí nhất định trên Trái Đất, gây ra hiện tượng thủy triều lên và xuống.
- Chuyển động của các hành tinh: Cường độ trường hấp dẫn giữa Mặt Trời và các hành tinh duy trì quỹ đạo của chúng. Các hành tinh chuyển động theo quỹ đạo hình elip quanh Mặt Trời dưới tác động của lực hấp dẫn, là một trong các định lý về chuyển động của Kepler.
Những nghiên cứu về cường độ trường hấp dẫn và các hiện tượng liên quan đã cung cấp cơ sở quan trọng cho sự phát triển của vật lý thiên văn và các ngành khoa học khác, giúp giải thích các quy luật chuyển động của vật chất trong vũ trụ và ứng dụng trong việc phóng vệ tinh, tính toán quỹ đạo, và khám phá vũ trụ.
Đánh giá và củng cố kiến thức về cường độ trường hấp dẫn
Trong phần này, chúng ta sẽ ôn tập và củng cố những kiến thức quan trọng về cường độ trường hấp dẫn thông qua một số phương pháp học tập tích cực và hiệu quả. Hãy cùng thực hiện từng bước để làm rõ và hiểu sâu hơn về khái niệm, công thức và ứng dụng của cường độ trường hấp dẫn.
1. Ôn tập khái niệm và công thức
- Trường hấp dẫn là gì? Xác định lại khái niệm trường hấp dẫn và cường độ trường hấp dẫn tại một điểm.
- Nhắc lại công thức tính cường độ trường hấp dẫn: \[ g = \frac{GM}{R^2} \] trong đó \(G\) là hằng số hấp dẫn, \(M\) là khối lượng của vật tạo trường, và \(R\) là khoảng cách từ tâm vật đến điểm đang xét.
- Lưu ý: giá trị \(g\) là một đại lượng phụ thuộc vào khoảng cách và khối lượng của vật tạo trường.
2. Phân tích các yếu tố ảnh hưởng đến cường độ trường hấp dẫn
Các yếu tố chính tác động đến cường độ trường hấp dẫn bao gồm:
- Khối lượng vật tạo trường (M): Cường độ trường tỉ lệ thuận với khối lượng của vật tạo trường.
- Khoảng cách (R): Cường độ trường tỉ lệ nghịch với bình phương khoảng cách giữa điểm xét và vật tạo trường. Khi R tăng, cường độ trường sẽ giảm nhanh chóng.
3. Giải bài tập và tình huống thực tế
Để vận dụng và củng cố kiến thức, học sinh có thể giải các bài tập cụ thể và phân tích tình huống thực tế:
- Giải bài tập tính cường độ trường hấp dẫn tại các điểm khác nhau quanh Trái Đất và so sánh với các thiên thể khác.
- Phân tích các bài toán áp dụng định luật vạn vật hấp dẫn để tính lực hấp dẫn và so sánh cường độ trường ở các điểm gần và xa vật tạo trường.
4. Kiểm tra kiến thức qua câu hỏi trắc nghiệm và tự luận
| Loại câu hỏi | Mô tả |
|---|---|
| Trắc nghiệm | Kiểm tra nhanh các khái niệm cơ bản, cách áp dụng công thức và ý nghĩa của từng đại lượng trong công thức. |
| Tự luận | Giải thích cặn kẽ về cơ chế của trường hấp dẫn và cách cường độ trường thay đổi theo vị trí trong không gian. |
5. Luyện tập nâng cao
Để hiểu rõ hơn, học sinh có thể thực hiện các bài tập nâng cao, bao gồm:
- Phân tích và so sánh cường độ trường hấp dẫn của các thiên thể lớn như Mặt Trăng, Sao Hỏa với Trái Đất.
- Ứng dụng cường độ trường hấp dẫn trong việc tính toán quỹ đạo của các vệ tinh và ảnh hưởng của trường hấp dẫn đối với các hiện tượng thiên văn.
Qua các bước trên, học sinh có thể đánh giá và củng cố kiến thức về cường độ trường hấp dẫn, nâng cao kỹ năng giải bài tập và hiểu rõ hơn về vai trò của lực hấp dẫn trong các hiện tượng thiên văn và đời sống.