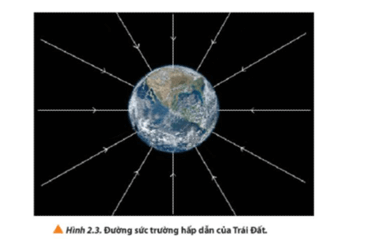
Chủ đề cường độ trường hấp dẫn gần bề mặt trái đất: Cường độ trường hấp dẫn gần bề mặt Trái Đất là một đại lượng vật lý quan trọng, giúp chúng ta hiểu rõ về lực hấp dẫn tác dụng lên các vật thể ở gần mặt đất. Bài viết này sẽ giới thiệu khái niệm, công thức tính toán, và những ứng dụng thực tế của cường độ trường hấp dẫn. Qua đó, bạn sẽ có cái nhìn sâu sắc hơn về vai trò của lực hấp dẫn trong đời sống hàng ngày cũng như trong các hiện tượng vật lý.
Mục lục
- Tổng quan về cường độ trường hấp dẫn
- Ứng dụng của cường độ trường hấp dẫn
- Định luật vạn vật hấp dẫn và mối quan hệ với cường độ trường hấp dẫn
- Thay đổi cường độ trường hấp dẫn theo độ cao
- Các yếu tố ảnh hưởng đến cường độ trường hấp dẫn của Trái Đất
- Cách đo lường và tính toán cường độ trường hấp dẫn
- Thế năng hấp dẫn trong trường hấp dẫn
- Các bài tập và câu hỏi thực hành về cường độ trường hấp dẫn
Tổng quan về cường độ trường hấp dẫn
Cường độ trường hấp dẫn là đại lượng đo lường lực tác dụng của một trường hấp dẫn lên một vật có khối lượng đơn vị. Đơn vị của cường độ trường hấp dẫn trong Hệ SI là newton trên kilogram (N/kg), biểu thị lực tác dụng lên mỗi kilogram của vật trong trường đó.
- Công thức cơ bản: Cường độ trường hấp dẫn \(g\) được tính bằng công thức:
\[
g = \frac{F}{m} = G \frac{M}{r^2}
\]
Trong đó:
- \(F\): Lực hấp dẫn tác dụng lên vật có khối lượng \(m\) (N)
- \(m\): Khối lượng của vật (kg)
- \(G\): Hằng số hấp dẫn \((6.674 \times 10^{-11} \, \text{N} \cdot \text{m}^2/\text{kg}^2)\)
- \(M\): Khối lượng của thiên thể (kg)
- \(r\): Khoảng cách từ tâm thiên thể đến vật (m)
- Cường độ trường hấp dẫn tại bề mặt Trái Đất: Trên bề mặt Trái Đất, gia tốc trọng trường trung bình khoảng \(g \approx 9.81 \, \text{m/s}^2\). Con số này có thể thay đổi đôi chút do sự khác biệt về độ cao, mật độ vật chất và vĩ độ địa lý.
- Sự phụ thuộc vào độ cao:
Khi độ cao tăng lên, cường độ trường hấp dẫn giảm đi theo công thức:
\[
g_h = g_0 \left(\frac{R}{R + h}\right)^2
\]
Trong đó:
- \(g_0\): Cường độ trường hấp dẫn tại mặt đất.
- \(R\): Bán kính của Trái Đất.
- \(h\): Độ cao so với mặt đất.
Ví dụ, tại độ cao của Trạm Vũ trụ Quốc tế (khoảng 420 km so với mặt đất), cường độ trường hấp dẫn chỉ còn khoảng 8.63 N/kg, nhỏ hơn so với trên mặt đất.
- Ứng dụng thực tế:
- Cường độ trường hấp dẫn là yếu tố quan trọng trong việc tính toán các quỹ đạo của vệ tinh và tàu vũ trụ.
- Hiểu rõ sự thay đổi của \(g\) giúp cải thiện độ chính xác trong các ứng dụng khoa học và kỹ thuật, như dự báo chuyển động của vật thể trong không gian.
Các khái niệm và công thức liên quan đến cường độ trường hấp dẫn là nền tảng quan trọng trong vật lý thiên văn, giúp giải thích nhiều hiện tượng tự nhiên và các hiện tượng vật lý cơ bản.
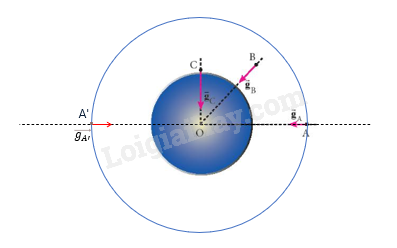
Ứng dụng của cường độ trường hấp dẫn
Cường độ trường hấp dẫn có vai trò quan trọng trong nhiều lĩnh vực khoa học và ứng dụng thực tiễn. Các ứng dụng bao gồm từ đo lường địa vật lý, nghiên cứu vũ trụ, đến các công nghệ vệ tinh hiện đại. Dưới đây là một số ứng dụng tiêu biểu:
- Đo lường địa vật lý và nghiên cứu động đất: Đo lường cường độ trường hấp dẫn tại các điểm khác nhau trên bề mặt Trái Đất giúp phát hiện sự thay đổi trong khối lượng và mật độ địa tầng, hỗ trợ nghiên cứu và cảnh báo động đất. Những thay đổi nhỏ trong cường độ trường hấp dẫn có thể tiết lộ sự dịch chuyển của mảng kiến tạo.
- Hệ thống định vị toàn cầu (GPS): Cường độ trường hấp dẫn ảnh hưởng đến hoạt động của các vệ tinh GPS, vì vậy việc tính toán cẩn thận giúp hệ thống GPS duy trì độ chính xác cao trong định vị và dẫn đường. Các kỹ thuật GPS tiên tiến cần điều chỉnh tác động của trường hấp dẫn để tối ưu hóa tín hiệu vệ tinh và độ chính xác của tọa độ.
- Khảo sát và khai thác tài nguyên: Trường hấp dẫn được sử dụng trong thăm dò khoáng sản và dầu mỏ. Các nhà địa chất sử dụng các biến đổi trong cường độ hấp dẫn để xác định các khu vực có mật độ vật chất cao hơn, giúp xác định vị trí tài nguyên quý như dầu, khí đốt và khoáng sản.
- Ngành hàng không vũ trụ: Hiểu biết về cường độ trường hấp dẫn giúp tính toán quỹ đạo bay và điều hướng của vệ tinh, tàu vũ trụ. Khi vệ tinh và các trạm không gian quay quanh Trái Đất, chúng chịu tác động của lực hấp dẫn, ảnh hưởng đến tốc độ và quỹ đạo của chúng, đòi hỏi điều chỉnh thường xuyên để duy trì đúng vị trí trong không gian.
- Ứng dụng trong đời sống và công nghệ: Cường độ trường hấp dẫn còn được ứng dụng trong các thiết bị đo trọng lực, đặc biệt trong các nghiên cứu về sức khỏe và thể chất trong môi trường không trọng lực, như trên trạm vũ trụ. Từ các nghiên cứu này, các biện pháp hỗ trợ sức khỏe và thể lực của phi hành gia được phát triển để giảm thiểu tác động tiêu cực của môi trường không trọng lực.
Định luật vạn vật hấp dẫn và mối quan hệ với cường độ trường hấp dẫn
Định luật vạn vật hấp dẫn, do Isaac Newton đề xuất, là một trong những nguyên lý nền tảng của vật lý cổ điển. Định luật này chỉ ra rằng mọi vật thể trong vũ trụ đều hút lẫn nhau với một lực tỷ lệ thuận với tích khối lượng của chúng và tỷ lệ nghịch với bình phương khoảng cách giữa chúng. Công thức toán học của lực hấp dẫn giữa hai vật thể có khối lượng \(m_1\) và \(m_2\), cách nhau một khoảng cách \(r\), được viết như sau:
- \(F = G \frac{{m_1 \cdot m_2}}{{r^2}}\)
Trong đó, \(F\) là lực hấp dẫn, \(G\) là hằng số hấp dẫn (\(6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2\)). Hệ quả từ công thức này là lực hấp dẫn yếu dần khi khoảng cách tăng, điều này giúp giải thích hiện tượng trọng lực giảm dần khi lên cao trên bề mặt Trái Đất.
Cường độ trường hấp dẫn, kí hiệu \(g\), mô tả gia tốc do lực hấp dẫn gây ra lên một vật thể đặt tại vị trí đó. Cường độ này có thể được định nghĩa bằng công thức:
- \(g = \frac{F}{m} = G \frac{M}{R^2}\)
Ở đây, \(M\) là khối lượng của Trái Đất và \(R\) là khoảng cách từ tâm Trái Đất đến vị trí tính toán. Nhờ định nghĩa này, ta có thể tính cường độ trường hấp dẫn tại bề mặt Trái Đất là xấp xỉ \(9.81 \, \text{m/s}^2\).
Mối quan hệ giữa định luật vạn vật hấp dẫn và cường độ trường hấp dẫn rất rõ ràng: cường độ trường hấp dẫn tại một điểm chính là lực hấp dẫn tác dụng trên một đơn vị khối lượng tại điểm đó. Như vậy, cường độ trường hấp dẫn được xem như một biểu hiện của lực hấp dẫn trong không gian quanh một vật thể lớn như Trái Đất.
Theo các nghiên cứu, cường độ trường hấp dẫn còn có liên hệ mật thiết với độ cao, dẫn đến sự biến thiên nhỏ trong gia tốc trọng trường khi di chuyển lên cao (ví dụ tại đỉnh Everest hay trạm ISS). Nhờ hiểu rõ mối quan hệ này, con người có thể ứng dụng vào việc thiết kế tàu vũ trụ và dự báo hiện tượng thiên văn như quỹ đạo của các hành tinh và vệ tinh.
Thay đổi cường độ trường hấp dẫn theo độ cao
Cường độ trường hấp dẫn, thường biểu diễn qua gia tốc rơi tự do \( g \), phụ thuộc vào khoảng cách từ vật đến tâm Trái Đất. Khi độ cao tăng, khoảng cách từ bề mặt Trái Đất đến vật cũng tăng, làm giảm cường độ trường hấp dẫn theo quy luật nghịch đảo bình phương. Để hiểu rõ hơn, ta xem xét công thức tính cường độ trường hấp dẫn tại độ cao \( h \):
\[
g_h = \frac{GM}{(R + h)^2}
\]
Trong đó:
- \( g_h \): cường độ trường hấp dẫn tại độ cao \( h \).
- \( G \): hằng số hấp dẫn (khoảng \(6.674 \times 10^{-11} \, \text{N}\cdot\text{m}^2/\text{kg}^2\)).
- \( M \): khối lượng của Trái Đất.
- \( R \): bán kính trung bình của Trái Đất (khoảng \(6,371 \, \text{km}\)).
- \( h \): độ cao tính từ mặt đất đến điểm cần tính \( g_h \).
Theo công thức trên, khi \( h \) tăng lên, giá trị \( g_h \) giảm, nghĩa là cường độ trường hấp dẫn suy yếu. Ví dụ, cường độ tại đỉnh Fansipan (cao 3,143 m) giảm khoảng 1%, trong khi tại Trạm Không Gian Quốc Tế (ISS), cường độ này giảm tới 11% so với mặt đất.
Để hiểu rõ hơn, bảng dưới đây minh họa sự thay đổi của \( g \) khi thay đổi độ cao \( h \):
| Độ cao (m) | Cường độ trường hấp dẫn (\( m/s^2 \)) | Giảm so với mặt đất (%) |
|---|---|---|
| 0 (mặt đất) | 9.81 | 0% |
| 3,143 (đỉnh Fansipan) | 9.72 | 1% |
| 370,000 (quỹ đạo ISS) | 8.77 | 11% |
Như vậy, cường độ trường hấp dẫn gần bề mặt Trái Đất giảm dần theo độ cao, điều này ảnh hưởng lớn đến trọng lượng của vật thể và là yếu tố quan trọng trong thiết kế các nhiệm vụ không gian và dự đoán chuyển động của các vật thể ngoài khí quyển Trái Đất.
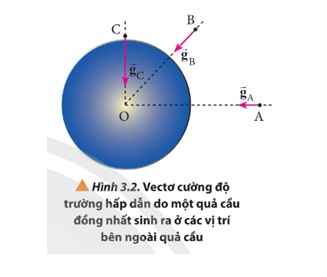
Các yếu tố ảnh hưởng đến cường độ trường hấp dẫn của Trái Đất
Cường độ trường hấp dẫn trên bề mặt Trái Đất có thể thay đổi do nhiều yếu tố khác nhau. Dưới đây là một số yếu tố chính ảnh hưởng đến giá trị của nó:
- Khối lượng của Trái Đất: Khối lượng là yếu tố quyết định trực tiếp đến cường độ trường hấp dẫn, với công thức \( g = \frac{GM}{R^2} \). Do đó, bất kỳ thay đổi nào trong phân bố khối lượng của Trái Đất cũng có thể làm thay đổi giá trị \( g \) tại các điểm trên bề mặt.
- Độ cao so với mực nước biển: Khi một vật di chuyển lên độ cao h, khoảng cách giữa vật và tâm Trái Đất tăng lên, làm giảm cường độ trường hấp dẫn. Giá trị này có thể tính bằng công thức \( g' = g \left( 1 - \frac{2h}{R} \right) \) khi \( h \) nhỏ so với bán kính Trái Đất \( R \).
- Địa hình và mật độ địa chất: Tại những khu vực có mật độ địa chất cao (như vùng đá cứng hoặc khoáng sản), giá trị cường độ trường hấp dẫn sẽ cao hơn so với các khu vực có mật độ thấp hơn. Sự chênh lệch trong địa hình, chẳng hạn như núi cao hoặc vùng lòng chảo, cũng làm thay đổi giá trị \( g \) ở các vị trí địa lý khác nhau.
- Sự tự quay của Trái Đất: Sự tự quay tạo ra lực ly tâm, làm giảm nhẹ cường độ trường hấp dẫn tại các điểm gần xích đạo so với các điểm ở cực. Tác động này khiến giá trị \( g \) ở xích đạo nhỏ hơn ở hai cực, với chênh lệch khoảng 0.03 m/s2.
Như vậy, cường độ trường hấp dẫn của Trái Đất không phải là một giá trị cố định mà thay đổi linh hoạt tùy vào vị trí và các yếu tố tự nhiên. Hiểu rõ các yếu tố này giúp con người ứng dụng hiệu quả trong các ngành khoa học như địa lý, khảo sát và không gian học.
Cách đo lường và tính toán cường độ trường hấp dẫn
Việc đo lường và tính toán cường độ trường hấp dẫn (\(g\)) là một phần quan trọng trong nghiên cứu vật lý và khoa học ứng dụng, vì nó cung cấp thông tin về lực hấp dẫn tác động lên vật thể trên Trái Đất. Để tính toán, ta có thể sử dụng công thức liên hệ cường độ trường hấp dẫn với định luật vạn vật hấp dẫn của Newton:
\[ g = \frac{GM}{R^2} \]
Trong đó:
- \(G\) là hằng số hấp dẫn với giá trị khoảng \(6.674 \times 10^{-11} \, \text{N(m/kg)}^2\),
- \(M\) là khối lượng của Trái Đất, khoảng \(5.97 \times 10^{24} \, \text{kg}\),
- \(R\) là bán kính từ tâm Trái Đất đến điểm cần tính cường độ hấp dẫn.
Các bước cụ thể để đo lường và tính toán bao gồm:
- Xác định vị trí của điểm đo lường (độ cao \(h\) so với mực nước biển hoặc khoảng cách từ tâm Trái Đất),
- Thu thập các dữ liệu cần thiết về khối lượng Trái Đất (\(M\)), hằng số hấp dẫn (\(G\)), và bán kính Trái Đất tại điểm đo.
- Thay các giá trị này vào công thức trên để tính \(g\) tại độ cao xác định hoặc trên bề mặt Trái Đất, khi \(R \approx 6,371 \, \text{km}\).
Ở một số khu vực, \(g\) có thể được đo trực tiếp bằng các thiết bị như gia tốc kế hoặc sử dụng con lắc đơn, trong đó độ dài và chu kỳ dao động của con lắc cho phép tính gia tốc trọng trường:
\[ g = \frac{4\pi^2L}{T^2} \]
Trong đó:
- \(L\) là chiều dài con lắc,
- \(T\) là chu kỳ dao động của con lắc.
Phương pháp sử dụng con lắc đơn thường được ứng dụng trong thí nghiệm ở trường học do tính chính xác và dễ thực hiện. Các phép đo này rất hữu ích trong việc kiểm tra và xác nhận sự thay đổi cường độ hấp dẫn theo độ cao hoặc vị trí địa lý.
Thế năng hấp dẫn trong trường hấp dẫn
Thế năng hấp dẫn là năng lượng tiềm tàng mà một vật sở hữu do vị trí của nó trong trường hấp dẫn. Trong trường hợp của Trái Đất, thế năng hấp dẫn được tính toán dựa trên độ cao của vật thể so với một mức độ tham chiếu, thường là mặt đất hoặc mặt nước biển.
Công thức tính thế năng hấp dẫn (\(U\)) được thể hiện như sau:
\[ U = mgh \]
Trong đó:
- \(U\) là thế năng hấp dẫn (Joule),
- \(m\) là khối lượng của vật thể (kg),
- \(g\) là cường độ trường hấp dẫn tại vị trí đó (m/s²),
- \(h\) là độ cao của vật thể so với mực nước biển (m).
Thế năng hấp dẫn có vai trò quan trọng trong nhiều lĩnh vực, như:
- Vật lý và cơ học: Giúp giải thích chuyển động của vật thể trong trường hấp dẫn, ví dụ như việc các vật thể rơi tự do hoặc bay lên cao.
- Kỹ thuật: Ứng dụng trong thiết kế cầu, đập, và các công trình xây dựng khác, nơi cần tính toán tác động của trọng lực lên các cấu trúc.
- Thiên văn học: Giúp hiểu rõ hơn về lực hấp dẫn giữa các hành tinh, sao và các vật thể trong không gian.
Khi một vật được nâng lên cao hơn, thế năng hấp dẫn của nó tăng lên, và ngược lại, khi nó rơi xuống, thế năng giảm đi. Điều này có thể được nhìn thấy trong các thí nghiệm thực tiễn như việc thả một vật từ độ cao, nơi mà thế năng chuyển hóa thành động năng khi vật rơi xuống.
Tóm lại, thế năng hấp dẫn là một khái niệm cơ bản trong vật lý, giúp chúng ta hiểu và tính toán năng lượng của các vật thể trong trường hấp dẫn của Trái Đất.
Các bài tập và câu hỏi thực hành về cường độ trường hấp dẫn
Dưới đây là một số bài tập và câu hỏi thực hành giúp người học hiểu rõ hơn về cường độ trường hấp dẫn gần bề mặt Trái Đất:
-
Bài tập 1:
Tính cường độ trường hấp dẫn (\(g\)) tại bề mặt Trái Đất.
Dữ liệu: Khối lượng Trái Đất \(M = 5.97 \times 10^{24} \, \text{kg}\), bán kính Trái Đất \(R = 6,371 \, \text{km}\).
Hướng dẫn: Sử dụng công thức:
\[ g = \frac{GM}{R^2} \]
để tính toán. -
Bài tập 2:
Một vật có khối lượng 10 kg được thả từ độ cao 5 m. Tính thế năng hấp dẫn (\(U\)) của vật này tại vị trí thả.
Dữ liệu: Sử dụng \(g \approx 9.81 \, \text{m/s}^2\).
Hướng dẫn: Sử dụng công thức:
\[ U = mgh \]
để tính toán. -
Bài tập 3:
Tính cường độ trường hấp dẫn (\(g\)) ở độ cao 1.5 km so với mặt đất.
Dữ liệu: Sử dụng cùng giá trị khối lượng và bán kính của Trái Đất.
Hướng dẫn: Thay đổi bán kính \(R\) thành \(R + h\) trong công thức.
- Câu hỏi 1: Giải thích ý nghĩa của cường độ trường hấp dẫn và tại sao nó quan trọng trong vật lý.
- Câu hỏi 2: Nêu rõ cách mà thế năng hấp dẫn được chuyển đổi thành động năng khi một vật rơi tự do.
- Câu hỏi 3: Tại sao cường độ trường hấp dẫn ở các vị trí khác nhau trên Trái Đất lại khác nhau? Nêu ví dụ.
Những bài tập và câu hỏi này sẽ giúp bạn nâng cao kiến thức về cường độ trường hấp dẫn và ứng dụng của nó trong thực tiễn.