Bài 3 Thế Hấp Dẫn và Thế Năng Hấp Dẫn: Khái Niệm và Ứng Dụng Trong Vật Lý 11

Thế hấp dẫn và trường hấp dẫn là hai khái niệm cơ bản trong vật lý giúp giải thích cách các vật thể tương tác với nhau qua lực hấp dẫn. Đây là nền tảng lý thuyết trong việc nghiên cứu chuyển động của các hành tinh, vệ tinh và cả hiện tượng liên quan đến trọng lực trên Trái Đất.

1.1. Khái niệm Thế Hấp Dẫn

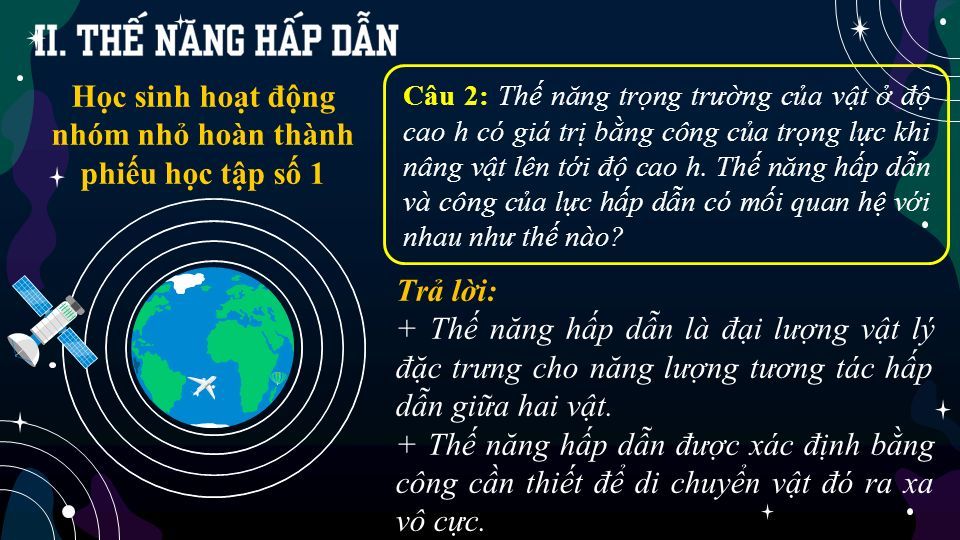
Thế hấp dẫn tại một điểm trong trường hấp dẫn là một đại lượng đo lường khả năng tác dụng lực hấp dẫn tại điểm đó. Nó giúp chúng ta xác định công mà lực hấp dẫn thực hiện khi một vật chuyển từ một điểm trong trường đến điểm gốc. Công thức tính thế hấp dẫn \( V \) của một vật khối lượng \( m \) trong trường hấp dẫn do một vật thể lớn hơn (như Trái Đất) gây ra có thể biểu diễn dưới dạng:

• \( V = - \dfrac{G \cdot M}{r} \)

Trong đó:

• \( G \) là hằng số hấp dẫn, giá trị là \( 6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2 \)
• \( M \) là khối lượng của vật thể gây ra trường hấp dẫn (ví dụ: khối lượng Trái Đất)
• \( r \) là khoảng cách từ tâm của vật gây ra trường hấp dẫn đến điểm đang xét

1.2. Khái niệm Trường Hấp Dẫn

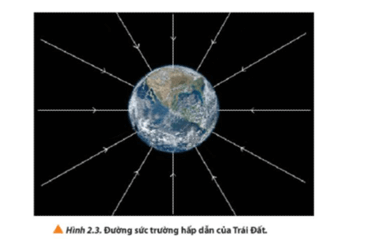
Trường hấp dẫn là không gian xung quanh một vật có khối lượng lớn, trong đó các vật thể khác chịu tác dụng của lực hấp dẫn. Cường độ của trường hấp dẫn tại một điểm cho biết độ lớn của lực hấp dẫn tác dụng lên một đơn vị khối lượng tại điểm đó. Công thức biểu diễn cường độ trường hấp dẫn \( g \) có dạng:

• \( g = \dfrac{G \cdot M}{r^2} \)

Trong đó:

• \( g \) là cường độ trường hấp dẫn
• \( r \) là khoảng cách từ tâm của vật gây ra trường đến điểm đang xét

1.3. Ví dụ Thực Tiễn

Ví dụ điển hình của trường hấp dẫn là lực hút của Trái Đất tác dụng lên các vật trên bề mặt. Nhờ đó, khi một vật được thả từ độ cao xuống, nó sẽ rơi theo chiều của lực hấp dẫn. Ngoài ra, hiểu về thế và trường hấp dẫn còn giúp con người tính toán và phóng vệ tinh vào quỹ đạo, đảm bảo vệ tinh không rơi trở lại Trái Đất nhờ đạt tốc độ quỹ đạo nhất định.

Thế năng hấp dẫn của một vật trong trường hấp dẫn phụ thuộc vào vị trí của vật và thường được xác định theo một điểm mốc, chẳng hạn như bề mặt Trái Đất hoặc một vị trí vô cùng xa nơi trường hấp dẫn không còn ảnh hưởng đáng kể.

Trong trường hấp dẫn của một vật thể lớn như Trái Đất, thế năng hấp dẫn \( W \) tại một điểm cách tâm của Trái Đất một khoảng \( r \) được xác định theo công thức:

\[
W = -G \frac{M \cdot m}{r}
\]

• Trong đó:
  • \( G \): hằng số hấp dẫn, \( G = 6.674 \times 10^{-11} \, \text{Nm}^2/\text{kg}^2 \).
  • \( M \): khối lượng của vật tạo ra trường hấp dẫn (như Trái Đất).
  • \( m \): khối lượng của vật chịu ảnh hưởng của trường hấp dẫn.
  • \( r \): khoảng cách từ tâm vật tạo trường đến vị trí của vật chịu lực hấp dẫn.

Đơn vị của thế năng hấp dẫn là Joules (J), và giá trị thế năng này thường là âm. Điều này phản ánh rằng để di chuyển một vật từ vị trí này ra xa khỏi trường hấp dẫn đến vô cùng (nơi thế năng là 0), cần cung cấp một công dương bằng trị số tuyệt đối của thế năng tại vị trí hiện tại.

2.1 Mối Quan Hệ Giữa Thế Năng và Công Của Trọng Lực

Khi một vật di chuyển từ vị trí có thế năng \( W_1 \) đến vị trí có thế năng \( W_2 \), công của lực hấp dẫn tác động lên vật sẽ được tính là:

\[
A = W_1 - W_2
\]

Do đó, nếu vật rơi từ một độ cao xuống, công của trọng lực sẽ dương vì thế năng giảm, còn nếu nâng vật lên, công sẽ âm do cần cung cấp năng lượng để khắc phục lực hấp dẫn.

2.2 Ứng Dụng của Thế Năng Hấp Dẫn

• Trong các tính toán quỹ đạo của vệ tinh, thế năng giúp xác định năng lượng cần thiết để đưa một vệ tinh lên độ cao mong muốn và duy trì vị trí quỹ đạo.
• Thế năng hấp dẫn là cơ sở để giải thích nguyên lý làm việc của vệ tinh địa tĩnh, nơi mà tốc độ của vệ tinh quanh Trái Đất phải đủ để chống lại lực hấp dẫn kéo về.

Trong trường hấp dẫn, công của trọng lực là khái niệm quan trọng để hiểu sự di chuyển của các vật thể dưới tác động của lực hấp dẫn. Công của trọng lực khi một vật di chuyển từ vị trí này đến vị trí khác trong trường hấp dẫn được tính theo phương trình:

\[ W = F \cdot s \cdot \cos(\theta) \]

Trong đó:

• \( W \): Công của trọng lực (đơn vị Joule)
• \( F \): Độ lớn của lực trọng trường (Newton)
• \( s \): Quãng đường di chuyển của vật thể (mét)
• \( \theta \): Góc giữa phương của lực và hướng di chuyển của vật

Khi xét một vật thể rơi tự do trong trường hấp dẫn, công của trọng lực phụ thuộc vào khối lượng của vật thể và khoảng cách di chuyển. Với vật thể có khối lượng \( m \) nằm trong trường hấp dẫn có gia tốc \( g \), công của trọng lực khi vật di chuyển quãng đường \( h \) theo phương thẳng đứng có thể được biểu diễn như sau:

\[ W = m \cdot g \cdot h \]

Biểu thức này giúp xác định năng lượng cần thiết để nâng hoặc hạ vật thể trong trường hấp dẫn của Trái Đất. Khi vật thể chuyển động theo phương ngang, tức là góc \( \theta = 90^\circ \), công của trọng lực bằng không do thành phần của lực trọng lực theo phương ngang không thực hiện công.

Một số ứng dụng thực tế của công trọng lực bao gồm việc xác định năng lượng cần thiết cho vệ tinh thoát khỏi lực hút của Trái Đất, tính toán công trong hoạt động leo núi hoặc thả rơi tự do của các vật thể trong điều kiện thực tế.

Trong trường hấp dẫn, khái niệm lực thế liên quan đến đặc điểm của trọng lực. Lực thế là lực chỉ phụ thuộc vào vị trí của điểm đầu và điểm cuối mà không phụ thuộc vào đường đi thực tế của vật. Trường của một lực thế, như trọng lực, được gọi là trường thế. Điều này giúp đơn giản hóa cách tính toán công của trọng lực, vì công chỉ phụ thuộc vào vị trí khởi điểm và điểm kết thúc.

1. Đặc điểm của Lực Thế trong Trường Hấp Dẫn

• Lực thế không phụ thuộc vào đường đi mà vật thực hiện, chỉ phụ thuộc vào vị trí ban đầu và vị trí cuối cùng của vật.
• Công của lực thế khi dịch chuyển vật trong trường lực thế là một đại lượng xác định và không phụ thuộc vào quỹ đạo mà vật di chuyển.

2. Công Của Trọng Lực

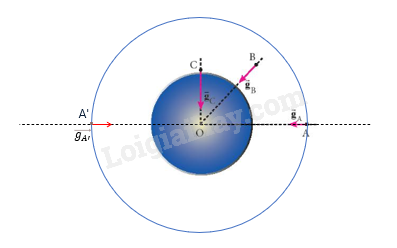
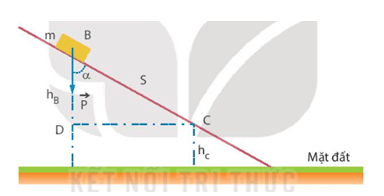
Công của trọng lực khi di chuyển vật có khối lượng m từ điểm B đến điểm C trong trường hấp dẫn có thể tính qua biểu thức:

\[ A_{B \to C} = W_t(B) - W_t(C) = m \cdot g \cdot (h_B - h_C) \]

Với:

• W_t(B): thế năng hấp dẫn tại điểm B.
• W_t(C): thế năng hấp dẫn tại điểm C.
• g: gia tốc trọng trường, thường là hằng số ở gần bề mặt Trái Đất.

3. Ứng dụng trong Đường Đi của Vật

Khi một vật chuyển động dưới tác dụng của lực thế, đường đi của vật sẽ phụ thuộc vào sự phân bố của trường thế và động năng ban đầu của vật. Nếu không có lực cản, vật sẽ di chuyển theo quỹ đạo tự do, chịu sự tác động của trường thế mà không mất năng lượng. Đối với các vật thể lớn trong không gian, như vệ tinh, đường đi của chúng trong trường hấp dẫn sẽ là một quỹ đạo nhất định như đường parabol, elip hoặc quỹ đạo tròn quanh hành tinh trung tâm.

4. Mặt Đẳng Thế

Trong trường hấp dẫn, các điểm có cùng thế năng tạo thành mặt đẳng thế. Đặc điểm quan trọng của mặt đẳng thế là:

• Mọi điểm trên một mặt đẳng thế đều có cùng thế năng.
• Trọng lực luôn vuông góc với mặt đẳng thế và hướng về phía có thế năng thấp hơn.
• Khoảng cách giữa các mặt đẳng thế trong trường hấp dẫn đều có xu hướng thu hẹp khi đến gần nguồn hấp dẫn hơn.

Nhờ vào việc sử dụng khái niệm mặt đẳng thế, chúng ta có thể dễ dàng tính toán lực và thế năng hấp dẫn tác dụng lên một vật tại các vị trí khác nhau trong trường.

Thế hấp dẫn và thế năng hấp dẫn không chỉ là những khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống, khoa học và công nghệ hiện đại. Những ứng dụng này đóng vai trò quan trọng trong việc phát triển kinh tế, bảo vệ môi trường và mở rộng hiểu biết về vũ trụ.

• Ứng dụng trong ngành năng lượng:

  Thế năng hấp dẫn được ứng dụng trong ngành thủy điện. Nước từ độ cao chảy xuống và thế năng hấp dẫn của nước được chuyển đổi thành động năng, tạo ra điện. Điều này giúp cung cấp năng lượng sạch cho các khu vực và góp phần giảm thiểu ô nhiễm môi trường.

• Vệ tinh và viễn thông:

  Các vệ tinh quay quanh Trái Đất hoạt động nhờ vào sự cân bằng giữa lực hấp dẫn của Trái Đất và tốc độ quỹ đạo của chúng. Thế năng hấp dẫn duy trì vệ tinh ở quỹ đạo, giúp chúng hoạt động ổn định trong việc truyền dữ liệu và viễn thông, hỗ trợ dự báo thời tiết và giám sát thiên tai.

• Khám phá không gian:

  Thế năng hấp dẫn là yếu tố quan trọng trong việc phóng tàu vũ trụ và đưa tàu về lại Trái Đất an toàn. Các nhà khoa học sử dụng kiến thức về thế năng hấp dẫn để tính toán lộ trình di chuyển của tàu vũ trụ, giúp thực hiện các nhiệm vụ khám phá Mặt Trăng, sao Hỏa và các hành tinh xa xôi khác.

• Công nghệ giao thông và vận tải:

  Các hệ thống vận tải như đường sắt cao tốc và các công nghệ mới như Hyperloop dựa vào việc tối ưu hóa năng lượng sử dụng từ thế năng và động năng để tăng hiệu quả di chuyển, giúp giảm chi phí vận hành và ô nhiễm.

• Nghiên cứu và bảo vệ Trái Đất:

  Thế năng hấp dẫn được sử dụng trong nghiên cứu địa chất và dự báo các chuyển động của mảng kiến tạo. Điều này giúp theo dõi và dự đoán hoạt động núi lửa, động đất và các hiện tượng địa chất khác, nhằm giảm thiểu rủi ro thiên tai cho con người.

Các bài tập về thế hấp dẫn và thế năng hấp dẫn là phần ứng dụng của lý thuyết để giúp học sinh hiểu sâu hơn về khái niệm và các định luật của lực hấp dẫn. Các dạng bài tập phổ biến bao gồm tính toán thế năng, công của trọng lực và chuyển động của vật trong trường hấp dẫn. Sau đây là một số dạng bài tập vận dụng thường gặp:

• Tính Thế Năng Hấp Dẫn
  1. Tính thế năng hấp dẫn của một vật có khối lượng \(m\) tại độ cao \(h\) so với mặt đất, khi cho gia tốc trọng trường \(g\) là hằng số.
  2. Xác định sự thay đổi thế năng khi vật chuyển động từ vị trí này sang vị trí khác trong trường hấp dẫn.
• Bài Tập Về Công của Trọng Lực
  1. Tính công của trọng lực khi một vật rơi tự do từ độ cao \(h_1\) xuống độ cao \(h_2\).
  2. Vận dụng công thức \(W = -\Delta W_t\) để tính toán công của trọng lực khi vật di chuyển trong trường hấp dẫn của Trái Đất.
• Bài Tập Về Chuyển Động Của Vật Trong Trường Hấp Dẫn
  1. Tính tốc độ cần thiết để một vật có thể thoát khỏi lực hút của Trái Đất (tốc độ vũ trụ cấp 1 và cấp 2).
  2. Giải các bài toán về chuyển động tròn đều của vệ tinh trong quỹ đạo địa tĩnh xung quanh Trái Đất.

Những bài tập trên giúp học sinh nắm vững các công thức và hiểu rõ hơn về lực hấp dẫn và ứng dụng của nó trong thực tế, từ đó củng cố kiến thức lý thuyết và phát triển tư duy khoa học.

Kiến thức về thế hấp dẫn và thế năng hấp dẫn không chỉ là những khái niệm cơ bản trong vật lý mà còn có tầm quan trọng lớn trong nhiều lĩnh vực khác nhau của cuộc sống. Hiểu biết về các lực hấp dẫn giúp chúng ta lý giải các hiện tượng tự nhiên, từ việc rơi tự do của vật thể đến sự chuyển động của các hành tinh trong hệ mặt trời.

Ngoài ra, kiến thức này còn có ứng dụng thiết thực trong kỹ thuật và công nghệ. Chẳng hạn, trong thiết kế các công trình kiến trúc, kỹ sư cần phải tính toán lực hấp dẫn để đảm bảo độ an toàn và độ bền cho công trình. Trong lĩnh vực hàng không vũ trụ, hiểu biết về lực hấp dẫn giúp xác định quỹ đạo của tàu vũ trụ và vệ tinh, từ đó tối ưu hóa quá trình phóng và điều khiển chúng.

Hơn nữa, việc nắm vững kiến thức về thế hấp dẫn còn góp phần phát triển tư duy phản biện và khả năng giải quyết vấn đề của học sinh. Qua các bài tập vận dụng, học sinh không chỉ ghi nhớ lý thuyết mà còn hình thành kỹ năng phân tích, đánh giá và ứng dụng kiến thức vào thực tiễn.

Tóm lại, thế hấp dẫn và thế năng hấp dẫn là những khái niệm thiết yếu trong vật lý, không chỉ hỗ trợ trong việc hiểu biết về tự nhiên mà còn mở ra nhiều cơ hội trong nghiên cứu và ứng dụng công nghệ. Việc nâng cao nhận thức và ứng dụng kiến thức này là rất cần thiết cho sự phát triển bền vững của xã hội.